Chapters 3–4: More search algorithms

DIT411/TIN175, Artificial Intelligence

Peter Ljunglöf

23 January, 2018

Table of contents

Heuristic search (R&N 3.5–3.6)

Greedy best-first search (3.5.1)

A* search (3.5.2)

Admissible/consistent heuristics (3.6–3.6.2)

The generic tree search algorithm

  • Tree search: Don’t check if nodes are visited multiple times
 
  • function Search(graph, initialState, goalState):
    • initialise frontier using the initialState
    • while frontier is not empty:
      • select and remove node from frontier
      • if node.state is a goalState then return node
      • for each child in ExpandChildNodes(node, graph):
        • add child to frontier
    • return failure

These are the two basic search algorithms

  • Depth-first search (DFS)
    • implement the frontier as a Stack
    • space complexity: \( O(bm) \)
    • incomplete: might fall into an infinite loop, doesn’t return optimal solution
  •  
  • Breadth-first search (BFS)
    • implement the frontier as a Queue
    • space complexity: \( O(b^m) \)
    • complete: always finds a solution, if there is one
    • (when edge costs are constant, BFS is also optimal)

Implement the frontier as a Priority Queue, ordered by \(f(n)\)

  • Uniform-cost search (this is not a heuristic algorithm)
    • expand the node with the lowest path cost
    • \( f(n) = g(n) \) = cost from start node to \(n\)
    • complete and optimal
  •  
  • Greedy best-first search
    • expand the node which is closest to the goal (according to some heuristics)
    • \( f(n) = h(n) \) = estimated cheapest cost from \(n\) to a goal
    • incomplete: might fall into an infinite loop, doesn’t return optimal solution
  •  
  • A* search
    • expand the node which has the lowest estimated cost from start to goal
    • \( f(n) = g(n) + h(n) \) = estimated cost of the cheapest solution through \(n\)
    • complete and optimal (if \(h(n)\) is admissible/consistent)

A* tree search is optimal!

  • A* always finds an optimal solution first, provided that:

    • the branching factor is finite,

    • arc costs are bounded above zero
      (i.e., there is some \(\epsilon>0\) such that all
      of the arc costs are greater than \(\epsilon\)), and

    • \(h(n)\) is admissible

    • i.e., \(h(n)\) is nonnegative and an underestimate of
      the cost of the shortest path from \(n\) to a goal node.

The generic graph search algorithm

  • Tree search: Don’t check if nodes are visited multiple times
  • Graph search: Keep track of visited nodes
 
  • function Search(graph, initialState, goalState):
    • initialise frontier using the initialState
    • initialise exploredSet to the empty set
    • while frontier is not empty:
      • select and remove node from frontier
      • if node.state is a goalState then return node
      • add node to exploredSet
      • for each child in ExpandChildNodes(node, graph):
        • add child to frontier if child is not in frontier or exploredSet
    • return failure

Graph-search = Multiple-path pruning

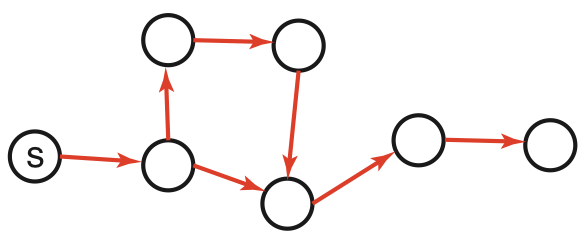
  • Graph search keeps track of visited nodes, so we don’t visit the same node twice.

    • Suppose that the first time we visit a node is not via the most optimal path

            \(\Rightarrow\)   then graph search will return a suboptimal path

    • Under which circumstances can we guarantee that A* graph search is optimal?

When is A* graph search optimal?

  • If  \( |h(n’)-h(n)| \leq cost(n’,n) \)  for every arc  \((n’,n)\),
    then A* graph search is optimal:
  •  
    • Lemma: the \(f\) values along any path \([…,n’,n,…]\) are nondecreasing:
      • Proof: \(g(n) = g(n’) + cost(n’, n)\), therefore:
      • \(f(n) = g(n) + h(n) = g(n’) + cost(n’, n) + h(n) \geq g(n’) + h(n’)\)
      • therefore: \(f(n) \geq f(n’)\), i.e., \(f\) is nondecreasing
  •  
    • Theorem: whenever A* expands a node \(n\), the optimal path to \(n\) has been found
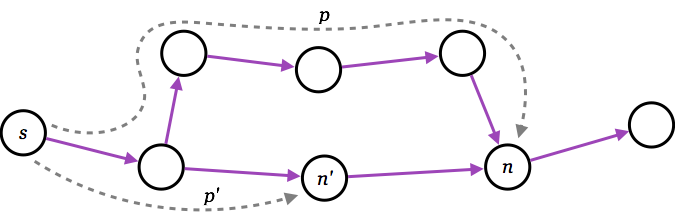      • Proof: Assume this is not true;
      • then there must be some \(n’\) still on the frontier, which is on the optimal path to \(n\);
      • but \(f(n’) \leq f(n)\);
      • and then \(n’\) must already have been expanded \(\Longrightarrow\) contradiction!

Consistency, or monotonicity

  • A heuristic function \(h\) is consistent (or monotone) if
    \( |h(m)-h(n)| \leq cost(m,n) \)   for every arc \((m,n)\)

    • (This is a form of triangle inequality)

    • If \(h\) is consistent, then A* graph search will always finds
      the shortest path to a goal.

    • This is a stronger requirement than admissibility.

Summary of optimality of A*

  • A* tree search is optimal if:

    • the heuristic function \(h(n)\) is admissible
    • i.e., \(h(n)\) is nonnegative and an underestimate of the actual cost
    • i.e., \( h(n) \leq cost(n,goal) \), for all nodes \(n\)

  • A* graph search is optimal if:

    • the heuristic function \(h(n)\) is consistent (or monotone)
    • i.e., \( |h(m)-h(n)| \leq cost(m,n) \), for all arcs \((m,n)\)

Summary of tree search strategies

Search
strategy		 Frontier
selection		 Halts if solution? Halts if no solution? Space usage
Depth first Last node added No No Linear
Breadth first First node added Yes No Exp
Greedy best first Minimal \(h(n)\) No No Exp
Uniform cost Minimal \(g(n)\) Optimal No Exp
A* \(f(n)=g(n)+h(n)\) Optimal* No Exp


*Provided that \(h(n)\) is admissible.

  • Halts if: If there is a path to a goal, it can find one, even on infinite graphs.
  • Halts if no: Even if there is no solution, it will halt on a finite graph (with cycles).
  • Space: Space complexity as a function of the length of the current path.

Summary of graph search strategies

Search
strategy		 Frontier
selection		 Halts if solution? Halts if no solution? Space usage
Depth first Last node added (Yes)** Yes Exp
Breadth first First node added Yes Yes Exp
Greedy best first Minimal \(h(n)\) No Yes Exp
Uniform cost Minimal \(g(n)\) Optimal Yes Exp
A* \(f(n)=g(n)+h(n)\) Optimal* Yes Exp

**On finite graphs with cycles, not infinite graphs.
*Provided that \(h(n)\) is consistent.

  • Halts if: If there is a path to a goal, it can find one, even on infinite graphs.
  • Halts if no: Even if there is no solution, it will halt on a finite graph (with cycles).
  • Space: Space complexity as a function of the length of the current path.

Recapitulation: Heuristics for the 8 puzzle

  • \(h_{1}(n)\) = number of misplaced tiles
  • \(h_{2}(n)\) = total Manhattan distance
    (i.e., no. of squares from desired location of each tile)
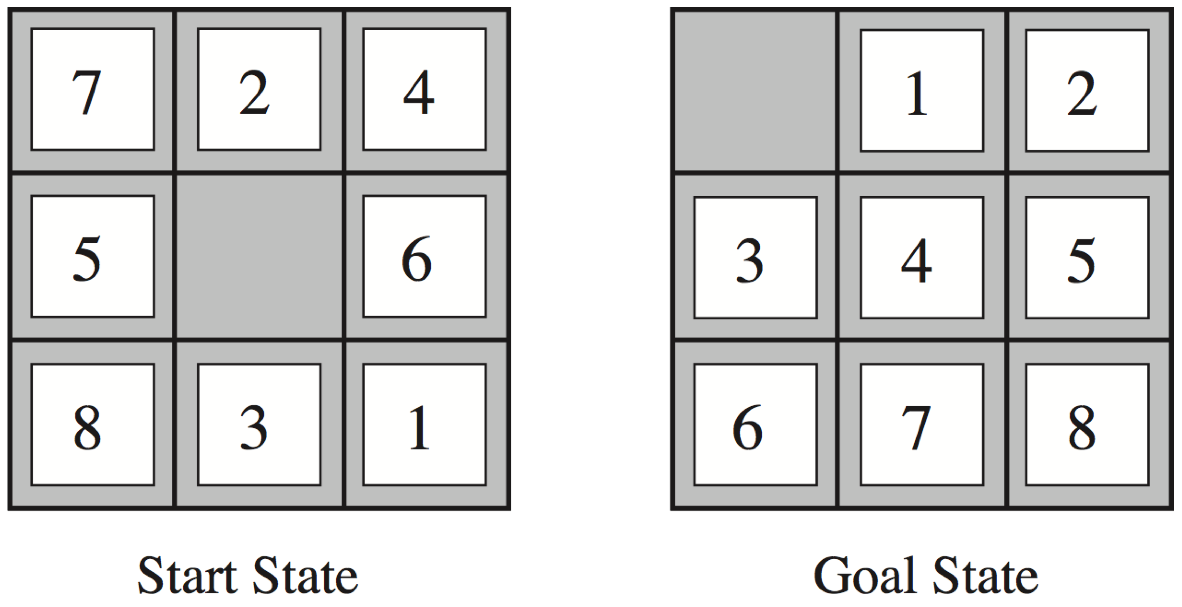
  • \(h_{1}(StartState)\)  =  8
  • \(h_{2}(StartState)\)  =  3+1+2+2+2+3+3+2 = 18

Dominating heuristics

  • If (admissible) \(h_{2}(n)\geq h_{1}(n)\) for all \(n\),
    then \(h_{2}\) dominates \(h_{1}\) and is better for search.

  • Typical search costs (for 8-puzzle):

    depth = 14 DFS  ≈  3,000,000 nodes
    A*(\(h_1\)) = 539 nodes
    A*(\(h_2\)) = 113 nodes
    depth = 24 DFS  ≈  54,000,000,000 nodes
    A*(\(h_1\)) = 39,135 nodes
    A*(\(h_2\)) = 1,641 nodes

  • Given any admissible heuristics \(h_{a}\), \(h_{b}\), the maximum heuristics \(h(n)\)
    is also admissible and dominates both: \[ h(n) = \max(h_{a}(n),h_{b}(n)) \]

Heuristics from a relaxed problem

  • Admissible heuristics can be derived from the exact solution cost of
    a relaxed problem:

    • If the rules of the 8-puzzle are relaxed so that a tile can move anywhere,
      then \(h_{1}(n)\) gives the shortest solution

    • If the rules are relaxed so that a tile can move to any adjacent square,
      then \(h_{2}(n)\) gives the shortest solution

  • Key point: the optimal solution cost of a relaxed problem is
    never greater than the optimal solution cost of the real problem

  • A* tree (graph) search with admissible (consistent) heuristics is optimal.

  • But what happens if the heuristics is non-admissible (non-consistent)?

    • i.e., what if \(h(n) > c(n,goal)\), for some \(n\)?*
    • the solution is not guaranteed to be optimal…
    • …but it will find some solution!

  • Why would we want to use a non-admissible heuristics?

    • sometimes it’s easier to come up with a heuristics that is almost admissible
    • and, often, the search terminates faster!

  •  

  • * for graph search, \( |h(m)-h(n)| > cost(m,n) \), for some \((m,n)\)

Example demo (again)

Here is an example demo of several different search algorithms, including A*.
Furthermore you can play with different heuristics:

http://qiao.github.io/PathFinding.js/visual/

Note that this demo is tailor-made for planar grids,
which is a special case of all possible search graphs.

More search strategies (R&N 3.4–3.5)

Iterative deepening (3.4.4–3.4.5)

Bidirectional search (3.4.6)

Memory-bounded heuristic search (3.5.3)

Iterative deepening

  • BFS is guaranteed to halt but uses exponential space.
    DFS uses linear space, but is not guaranteed to halt.

  • Idea: take the best from BFS and DFS — recompute elements of the frontier rather than saving them.

    • Look for paths of depth 0, then 1, then 2, then 3, etc.
    • Depth-bounded DFS can do this in linear space.

  • Iterative deepening search calls depth-bounded DFS with increasing bounds:

    • If a path cannot be found at depth-bound, look for a path at depth-bound + 1.
    • Increase depth-bound when the search fails unnaturally
      (i.e., if depth-bound was reached).

Iterative deepening example

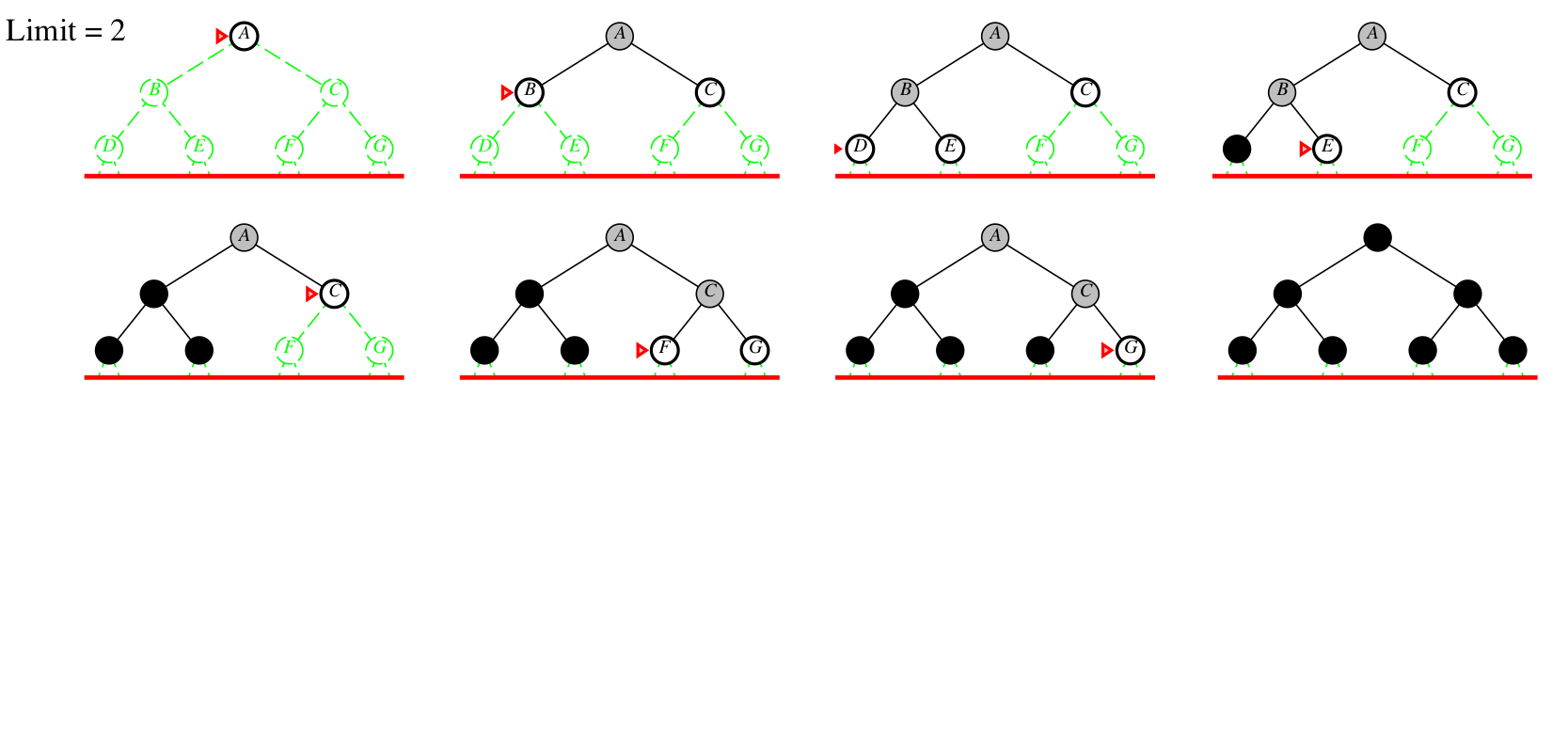
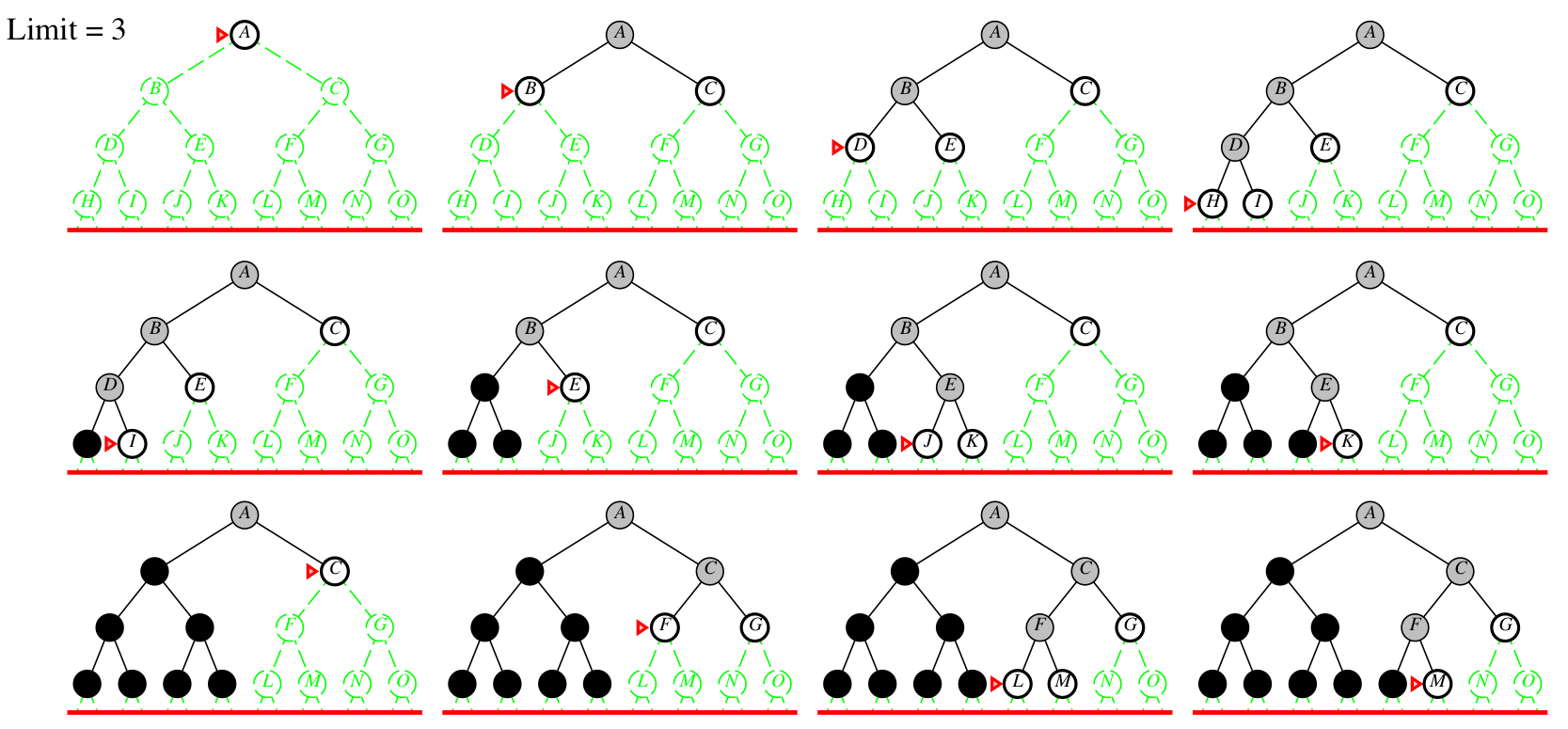
Depth bound = 0 1 2 3

  • function IDSearch(graph, initialState, goalState):
    • // returns a solution path, or ‘failure’
    • for limit in 0, 1, 2, …:
      • result := DepthLimitedSearch([initialState], limit)
      • if result ≠ cutoff then return result
  •  
  • function DepthLimitedSearch(\([n_{0},\dots,n_{k}]\), limit):
    • // returns a solution path, or ‘failure’ or ‘cutoff’
    • if \(n_{k}\) is a goalState then return path \([n_{0},\dots,n_{k}]\)
    • else if limit = 0 then return cutoff
    • else:
      • failureType := failure
      • for each neighbor \(n\) of \(n_{k}\):
        • result := DepthLimitedSearch(\([n_{0},\dots,n_{k},n]\), limit–1)
        • if result is a path then return result
        • else if result = cutoff then failureType := cutoff
      • return failureType

Iterative deepening complexity

Complexity with solution at depth \(k\) and branching factor \(b\):

level # nodes BFS node visits ID node visits
\(1\)
\(2\)
\(3\)
\(\vdots\)
\(k\)		 \(b\)
\(b^{2}\)
\(b^{3}\)
\(\vdots\)
\(b^{k}\)		 \(1\cdot b^{1}\)
\(1\cdot b^{2}\)
\(1\cdot b^{3}\)
\(\vdots\)
\(1\cdot b^{k}\)		 \(\,\,\,\,\,\,\,\,k\,\,\cdot b^{1}\)
\((k{-}1)\cdot b^{2}\)
\((k{-}2)\cdot b^{3}\)
\(\,\,\,\,\,\,\,\,\vdots\)
\(\,\,\,\,\,\,\,\,1\,\,\cdot b^{k}\)
total   \({}\geq b^{k}\) \({}\leq b^{k}\left(\frac{b}{b-1}\right)^{2}\)

Numerical comparison for \(k=5\) and \(b=10\):

  • BFS  =  10 + 100 + 1,000 + 10,000 + 100,000  =  111,110
  • IDS   =  50 + 400 + 3,000 + 20,000 + 100,000  =  123,450

Note: IDS recalculates shallow nodes several times,
but this doesn’t have a big effect compared to BFS!

Bidirectional search (3.4.6)

(will not be in the written examination, but could be used in Shrdlite)

  • The definition of searching is symmetric: find path from start nodes to goal node or from goal node to start nodes.

    • Forward branching factor: number of arcs going out from a node.

    • Backward branching factor: number of arcs going into a node.

  • Search complexity is \(O(b^{n})\).

    • Therefore, we should use forward search if forward branching factor is less than backward branching factor, and vice versa.

    • Note: if a graph is dynamically constructed, the backwards graph may not be available.

  • Idea: search backward from the goal and forward from the start simultaneously.

    • This can result in an exponential saving, because  \(2b^{k/2}\ll b^{k}\).

    • The main problem is making sure the frontiers meet.

  • One possible implementation:

    • Use BFS to gradually search backwards from the goal,
      building a set of locations that will lead to the goal.

      • this can be done using dynamic programming

    • Interleave this with forward heuristic search (e.g., A*)
      that tries to find a path to these interesting locations.

Memory-bounded A* (3.5.3)

(will not be in the written examination, but could be used in Shrdlite)

  • A big problem with A* is space usage — is there an iterative deepening version?

    • IDA*: use the \(f\) value as the cutoff cost
      • the cutoff is the smalles \(f\) value that exceeded the previous cutoff
      • often useful for problems with unit step costs
      • problem: with real-valued costs, it risks regenerating too many nodes
    • RBFS: recursive best-first search
      • similar to DFS, but continues along a path until \(f(n) > limit\)
      • \(limit\) is the \(f\) value of the best alternative path from an ancestor
      • if \(f(n) > limit\), recursion unwinds to alternative path
      • problem: regenerates too many nodes
    • SMA* and MA*: (simplified) memory-bounded A*
      • uses all available memory
      • when memory is full, it drops the worst leaf node from the frontier

Local search (R&N 4.1)

Hill climbing (4.1.1)

More local search (4.1.2–4.1.4)

Evaluating randomized algorithms

Iterative best improvement

  • In many optimization problems, the path is irrelevant
    • the goal state itself is the solution
  •  
  • Then the state space can be the set of “complete” configurations
    • e.g., for 8-queens, a configuration can be any board with 8 queens
      (it is irrelevant in which order the queens are added)
  •  
  • In such cases, we can use iterative improvement algorithms;
    we keep a single “current” state, and try to improve it
    • e.g., for 8-queens, we start with 8 queens on the board,
      and gradually move some queen to a better place
  •  
  • The goal would be to find an optimal configuration
    • e.g., for 8-queens, where no queen is threatened
  •  
  • Iterative improvement algorithms take constant space

Example: \(n\)-queens

  • Put \(n\) queens on an \(n\times n\) board, in separate columns

  • Move a queen to reduce the number of conflicts;
    repeat until we cannot move any queen anymore
         \(\Rightarrow\) then we are at a local maximum, hopefully it is global too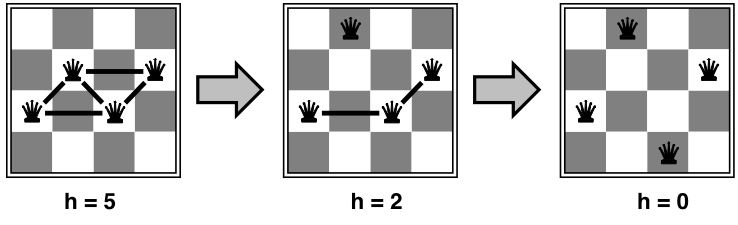

  • This almost always solves \(n\)-queens problems
    almost instantaneously for very large \(n\) (e.g., \(n\) = 1 million)

Example: 8-queens

 

  • Move a queen within its column, choose the minimum n:o of conflicts

    • the best moves are marked above (conflict value: 12)
    • after 5 steps we reach a local minimum (conflict value: 1)

Example: Travelling salesperson

  • Start with any complete tour, and perform pairwise exchanges

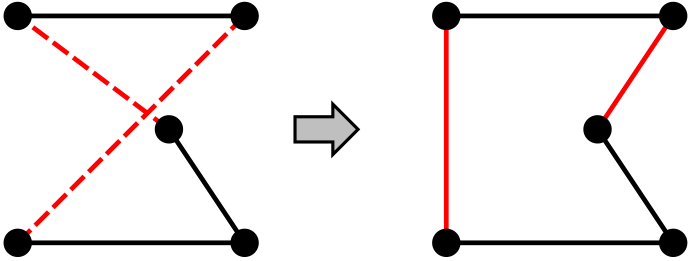
  • Variants of this approach can very quickly get
    within 1% of optimal solution for thousands of cities

Hill climbing search (4.1.1)

Also called (gradient/steepest) (ascent/descent),
or greedy local search

  • function HillClimbing(graph, initialState):
    • current := initialState
    • loop:
      • neighbor := a highest-valued successor of current
      • if neighbor.value ≤ current.value then return current
      • current := neighbor

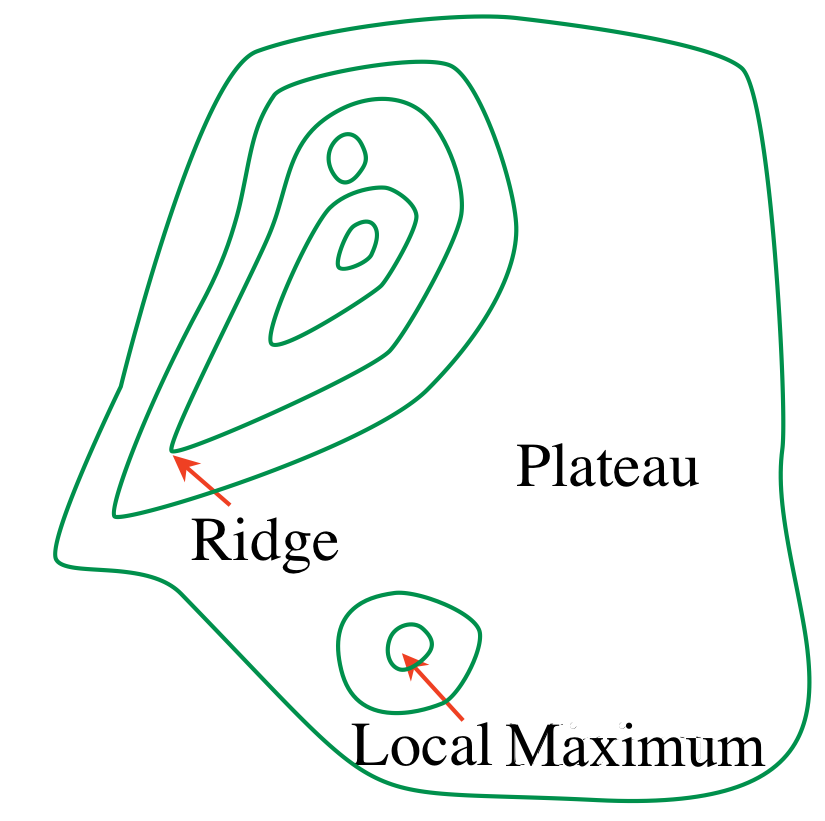
Problems with hill climbing

Local maxima   —   Ridges   —   Plateaux

    

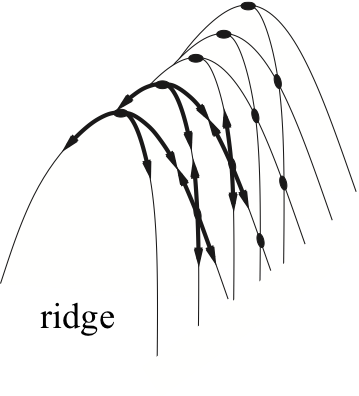
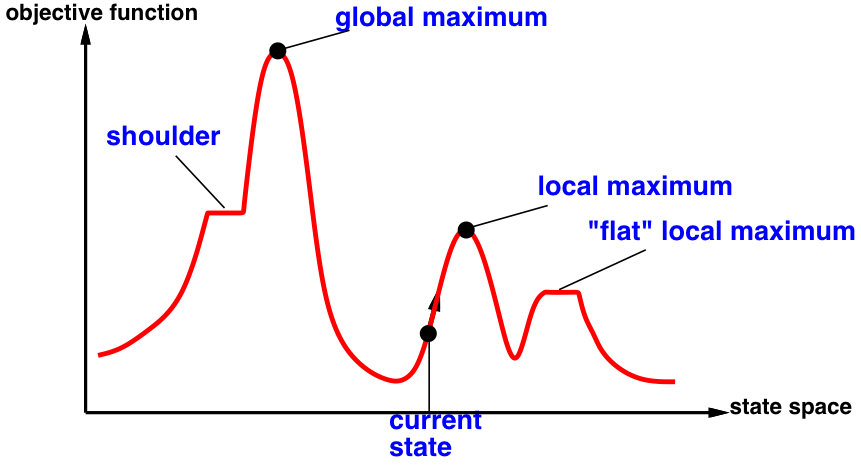
Randomized algorithms

  • Consider two methods to find a maximum value:

    • Greedy ascent: start from some position,
      keep moving upwards, and report maximum value found

    • Pick values at random, and report maximum value found

  • Which do you expect to work better to find a global maximum?

    • Can a mix work better?

Randomized hill climbing

  • As well as upward steps we can allow for:

    • Random steps: (sometimes) move to a random neighbor.

    • Random restart: (sometimes) reassign random values to all variables.

  • Both variants can be combined!

1-dimensional illustrative example

  • Two 1-dimensional search spaces; you can step right or left:

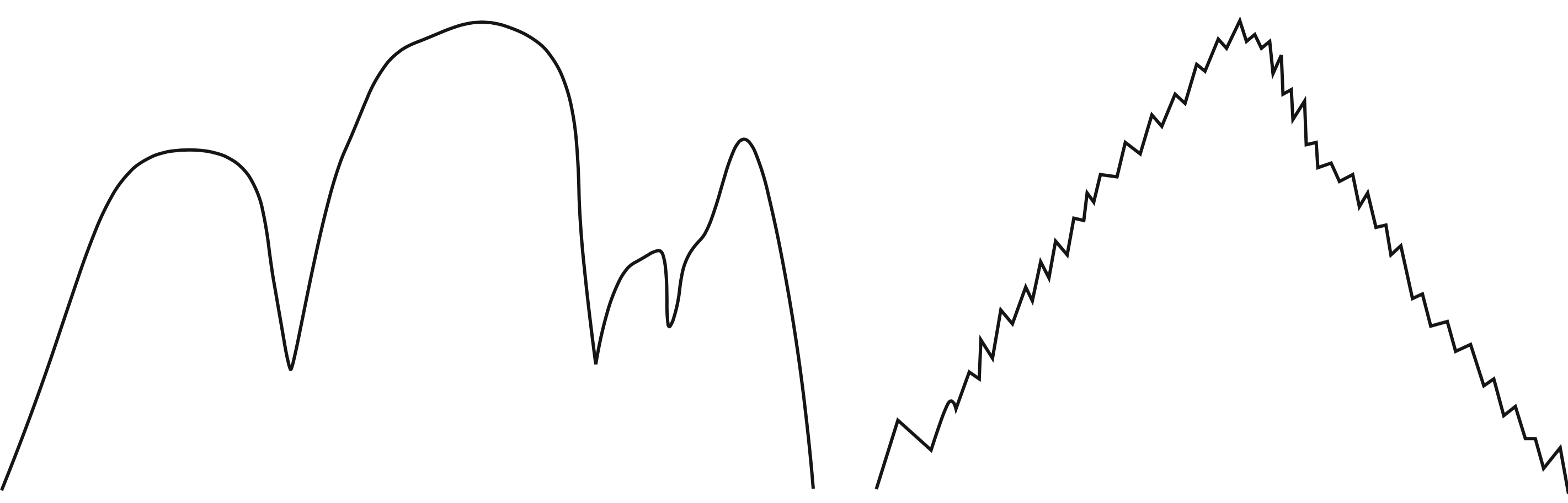
  • Which method would most easily find the global maximum?
    • random steps or random restarts?
  • What if we have hundreds or thousands of dimensions?
    • …where different dimensions have different structure?

(these sections will not be in the written examination)

Simulated annealing (4.1.2)

Beam search (4.1.3)

Genetic algorithms (4.1.4)

Simulated annealing (4.1.2)

Simulated annealing is an implementation of random steps:

  • function SimulatedAnnealing(problem, schedule):
    • current := problem.initialState
    • for t in 1, 2, …:
      • T := schedule(t)
      • if T = 0 then return current
      • next := a randomly selected neighbor of current
      • \(\Delta E\) := next.value – current.value
      • if \(\Delta E\) > 0 or with probability \(e^{\Delta E / T}\):
        • current := next

  • T is the “cooling temperature”, which decreases slowly towards 0

  • The cooling speed is decided by the schedule

Local beam search (4.1.3)

  • Idea: maintain a population of \(k\) states in parallel, instead of one.

    • At every stage, choose the \(k\) best out of all of the neighbors.
      • when \(k=1\), it is normal hill climbing search
      • when \(k=\infty\), it is breadth-first search

    • The value of \(k\) lets us limit space and parallelism.

    • Note: this is not the same as \(k\) searches run in parallel!

    • Problem: quite often, all \(k\) states end up on the same local hill.

Stochastic beam search (4.1.3)

  • Similar to beam search, but it chooses the next \(k\) individuals probabilistically.

    • The probability that a neighbor is chosen is proportional to its heuristic value.

    • This maintains diversity amongst the individuals.

    • The heuristic value reflects the fitness of the individual.

    • Similar to natural selection:
      each individual mutates and the fittest ones survive.

Genetic algorithms (4.1.4)

  • Similar to stochastic beam search,
    but pairs of individuals are combined to create the offspring.
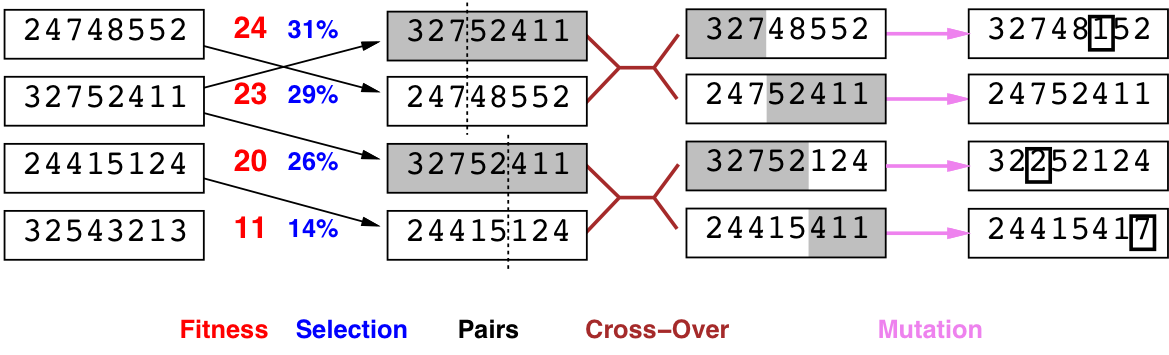
  • For each generation:
    • Randomly choose pairs of individuals where
      the fittest individuals are more likely to be chosen.
    • For each pair, perform a cross-over:
      form two offspring each taking different parts of their parents:
    • Mutate some values.
  • Stop when a solution is found.

\(n\)-queens encoded as a genetic algorithm

  • A solution to the \(n\)-queens problem can be encoded
    as a list of \(n\) numbers \(1\ldots n\):

Evaluating randomized algorithms (not in R&N)

(will not be in the written examination)

  • How can you compare three algorithms A, B and C, when

    • A solves the problem 30% of the time very quickly but doesn’t halt
      for the other 70% of the cases

    • B solves 60% of the cases reasonably quickly but doesn’t solve the rest

    • C solves the problem in 100% of the cases, but slowly?

  • Summary statistics, such as mean run time or median run time
    don’t make much sense.

Runtime distribution

Plots the runtime and the proportion of the runs that are solved within that runtime.