Natural Language Interpretation

DIT411/TIN175, Artificial Intelligence

Peter Ljunglöf

26 January, 2018

Table of contents

What is natural language?

  • Natural language

    • Any language that develops naturally in humans through use and repetition
      • e.g.: English, Swedish, Runyankole, Kangiryuarmiutun
    • Imprecisely defined: is “I totally lol’ed” correct?
    • Interpretation can be ambiguous

  • Formal language

    • Specifically constructed for some purpose, e.g.: Javascript, propositional logic
    • Precisely defined
      • print(1 + 2) ✅
      • print(+ 1 2. ❌
    • Unambiguous, precise semantics

Natural Language Processing (NLP)

  • Some examples of NLP tasks:

    • Information retrieval, e.g., web search
    • Machine translation, e.g. Google translate
    • Classification, e.g. sentiment analysis
    • Information extraction, e.g. Named entity recognition

Information retrieval

Machine translation

Classification

Sentiment analysis

https://www.csc.ncsu.edu/faculty/healey/tweet_viz

Information extraction

Named entity recognition

http://www.europeana-newspapers.eu/named-entity-recognition-for-digitised-newspapers

Approaches

  • Rules vs Statistics

    • Today many NLP tasks are powered by machine learning
    • We have lots of data (corpora), fast processors, cheap storage
    • Until the 1990s, most NLP systems were based on complex sets of hand-written rules

  • Does anyone use rule-based systems today?

    • Many NLP systems still use hand-written rules
    • E.g., domain-specific dialogue systems
      • Siri, Alexa, Cortana, …, use both hand-written rules and statistical NLP
      • …and not to forget Shrdlite!

Phrase-structure grammars

  • Words have different lexical categories:

    • noun, verb, adjective, prepositions, adverbs, …

  • We can combine them into phrasal categories:

    • “the” (determiner) + “ball” (noun) = “the ball” (noun phrase)
    • “in” (preposition) + “a box” (noun phrase) = “in a box” (prep. phrase)
    • “put” (verb) + “the ball” (noun phrase) + “in a box” (prep. phrase)
      = “put the ball in a box” (imperative sentence)

  • A grammar is a set of rules that describe which combinations are possible

    • “put a ball in a box on the floor” ✅
    • “put a ball in a box on the” ❌

Context-free grammars (CFG)

  • A Context-Free Grammar is a 4-tuple \(G = (V, \Sigma, R, S)\) where:

    • \(V\) is a finite set of non-terminals (called “syntactic categories”)
    • \(\Sigma\) is a finite set of terminals (disjoint from \(V\))
    • \(R\) is the set of production rules \(X\rightarrow\beta\),
      where \(X\in V\) and \(\beta\in(V \cup \Sigma)^*\)
    • \(S\in V\) is the start symbol

  • Common syntactic sugar:

    • \(X \rightarrow \alpha \;|\; \beta \;|\; \gamma\)   is the same as   \(X \rightarrow \alpha\),  \(X \rightarrow \beta\),  \(X \rightarrow \gamma\)

    • \(X \rightarrow \alpha? \; \beta \; \gamma?\)   is the same as   \(X \rightarrow \alpha \beta \gamma \;|\; \beta \gamma \;|\; \alpha \beta \;|\; \beta\)

Context-free grammar, example

A first attempt at a context-free grammar for Shrdlite:

  • Command   →   take   Entity   |   drop it   Location   |   move   Entity   Location
  • Entity   →   Quantifier   Object   |   the floor
  • Object   →   Size?   Color?   Form   |   Object   (that is)?   Location
  • Location   →   Relation   Entity
  • Quantifier   →   every   |   a   |   the   |   all
  • Size   →   large   |   small
  • Color   →   red   |   blue   |   white   |   black   |   …
  • Form   →   box   |   ball   |   pyramid   |   …   |   boxes   |   balls   |   pyramids   |   …
  • Relation   →   in   |   beside   |   under   |   …

  • This example grammar overgenerates:

    • “put every bricks on the floor”
    • “put all brick on the floor”

Handling agreement in CFG

  • CFG solution to overgeneration: add more rules

    • Entity   →   QuantifierSG   ObjectSG   |   QuantifierPL   ObjectPL   |   …
    • ObjectSG   →   Size?   Color?   FormSG   |   ObjectSG   (that is)?   Location
    • ObjectPL   →   Size?   Color?   FormPL   |   ObjectPL   (that are)?   Location
    • QuantifierSG   →   every   |   a   |   the
    • QuantifierPL   →   all
    • FormSG   →   box   |   ball   |   pyramid   |   …
    • FormPL   →   boxes   |   balls   |   pyramids   |   …

  • This is how we do it in Shrdlite.

Agreement and definite clause grammar

The CFG solution is not feasible for, e.g., German:

  • Entity   →   QuantFemNomSg ObjFemNomSg   |   QuantMascAckSg ObjMascAckSg   |   …
  • QuantFemNomSg   →   die
  • QuantMascAckSg   →   den
  • ColorFemNomSg   →   rote   |   blaue   |   …
  • ColorMascAccSg   →   roten   |   blauen   |   …

German has 2 × 3 × 4 = 24 combinations of Number, Gender and Case.
Definite-Clause Grammars use attributes and unification:

  • Entity   →   Quantifier[\(g,c,n\)]   Object[\(g,c,n\)]           \(\Longleftarrow\) Note! Only one rule
  • Quantifier[fem,nom,sg]   →   die
  • Quantifier[masc,acc,sg]   →   den
  • Color[fem,nom,sg]   →   rote   |   blaue   |   …
  • Color[masc,acc,sg]   →   roten   |   blauen   |  

Syntactic analysis (parsing)

  • Problem: Given a grammar, find a derivation from S for an input string

  • Function from string to a list of parse results:
    parse(g : Grammar, s : String) : Result[]

    • 0 results: input is invalid
    • 1 result: input is valid and unambiguous
    • 2+ results: input is valid and ambiguous

  • Algorithms:

    • Parsing can be formulated as a search problem
    • CKY algorithm, chart parsing, probabilistic parsing, …

Shrdlite parse results

The Nearley CFG formalism lets you specify how the parse results should look like:

  • Command   →   take   Entity                         { (d) => new TakeCommand(d[1]) }
  • Command   →   drop it   Location                { (d) => new DropCommand(d[2]) }
  • Command   →   move   Entity   Location    { (d) => new MoveCommand(d[1], d[2]) }

  • “put a green ball beside every large box”

  • \(\Longrightarrow\) MoveCommand(
                           Entity(“any”, SimpleObject(“ball”, null, “green”)),
                           Location(“beside”,
                                      Entity(“all”, SimpleObject(“box”, “large”, null))))

Syntactic ambiguity

  • “put a ball right of a box in a box beside a table”

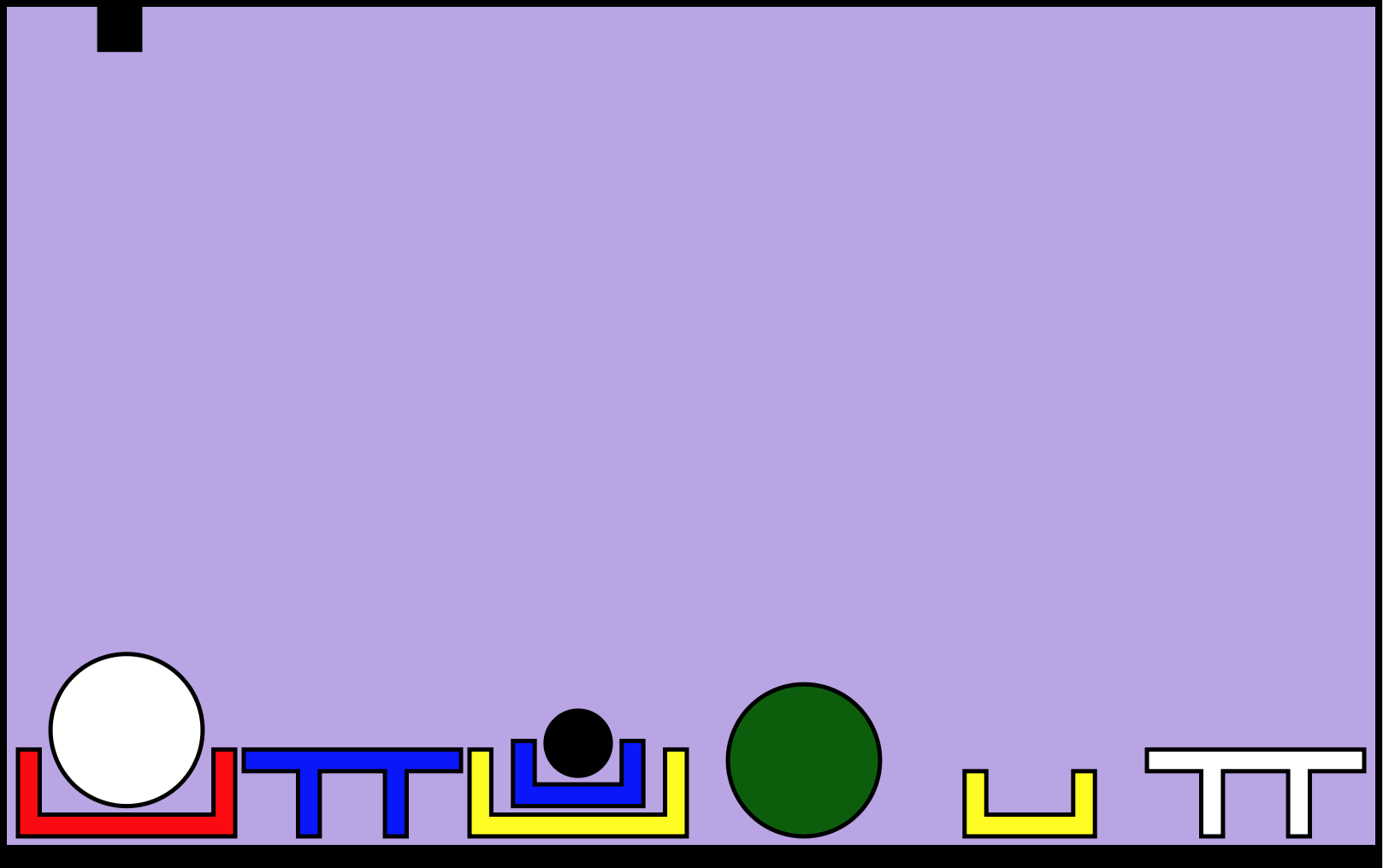
  • How many syntactic analyses?
  • “put (a ball) right of ((a box in a box) beside a table)”
  • “put (a ball) right of (a box in (a box beside a table))”
  • “put (a ball right of a box) in (a box beside a table)”
  • “put ((a ball right of a box) in a box) beside (a table)”
  • “put (a ball right of (a box in a box)) beside (a table)”

Levels of ambiguity

  • Most of the sentences we hear seem unambiguous. But almost every utterance contains some kinds of ambiguity. We are just very good at disambiguating!

  • Different levels of ambiguity:

    • Lexical: a word can belong to multiple categories
      • “Buffalo buffalo buffalo buffalo”
      • “Bison [from] Buffalo [often] confuse [other] bison”
    • Syntactic: Phrases can attach at different points in the tree
      • “I ordered a pizza with rucola”
      • “I ordered a pizza with my phone”
    • Semantic: Multiple interprations
      • “Everyone loves someone”
      • \(\forall x\exists y. Love(x,y)\)   or   \(\exists y\forall x. Love(x,y)\) ?

Why syntax, anyway?

  • So far, I’ve talked about grammars and parse results

    • but what do we do with them?
    • the parse results themselves are never our final goal

  • The next step is semantics (= interpretation)

    • statistical approaces:
      • e.g., named entitiy recognition, sentiment analysis, relation extraction
    • logical approaches:
      • e.g., predicate logic, lambda calculus, modal logic

Semantic representation, the Shrdlite way

  • Shrdlite semantics is propositional logic:

    • a logical description of how we want the final state to look like

      • one term for every object in the world:
        • WhiteBall, BlackBall, …
      • one predicate for every relation:
        • holding(x), inside(x,y), leftof(x,y), …
      • logical disjunction and conjunction instead of quantifiers:
        • P ∨ (Q ∧ R)

    • This works because the world is finite!

Interpretation, ambiguities

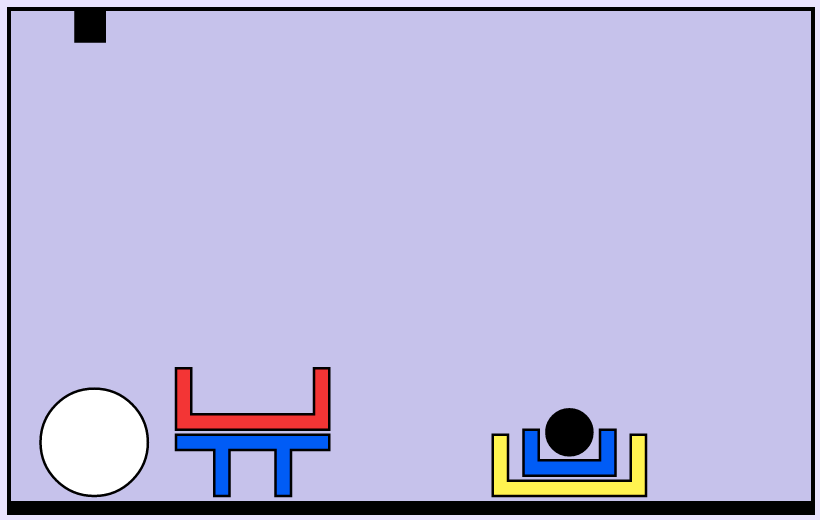
  • Is this ambiguous?      “put the white ball in the red box”

  • How about this?          “put the ball in the red box”

Shrdlite pipeline

  • This is how Shrdlite goes from text input to a final plan:

    1. Parsing: text input → (many) parse results
    2. Interpretation: parse result + world → (many) goals
    3. (Ambiguity resolution: many goals → one goal)
    4. Planning: goal → plan
    5. (Ambiguity resolution: many plans → one plan)

Parsing: text input \(\rightarrow{}\) parse results

  • function parse(input : string) : ShrdliteResult[]
    • (this function is already implemented)
  •  
  • interface ShrdliteResult {
    • input : string
    • parse : Command
    • interpretation : DNFFormula
    • plan : string[] }
  •  
  • This is already implemented using the Nearley grammar and parser
    • after parsing, every ShrdliteResult contains
      the input string and a parse result
    • the interpretation and plan are dummy values

Interpretation: parse result + world \(\rightarrow\) goals

  • function interpret(parses : ShrdliteResult[], world : WorldState) : ShrdliteResult[]
    • (this function is already implemented, but calls interpretCommand)
  •  
  • class Interpreter {
    • interpretCommand(cmd : Command) : CommandSemantics
    • interpretEntity(ent : Entity) : EntitySemantics
    • interpretLocation(loc : Location) : LocationSemantics
    • interpretObject(obj : Object) : ObjectSemantics }
  •  
  • This is what you have to implement in lab 2!
    • the Interpreter methods should call each other
    • what should the respective semantics be?

Semantics of commands: Disjunctive Normal Form

DNF = Disjunctive Normal Form = a disjunction of conjunctions of literals
(normal form = all logical formulae can be converted into this form)

  • type CommandSemantics = DNFFormula
  • class DNFFormula {
    • conjuncts : Conjunction[] }
  • class Conjunction {
    • literals : Literal[] }
  • class Literal {
    • relation : string
    • args : string[] = []
    • polarity : boolean = true }

Example: the formula (p(x) ∧ q) ∨ (¬r(y,z)) is created by:

  • new DNFFormula([
    • new Conjunction([new Literal(“p”, [“x”]), new Literal(“q”)]),
    • new Conjunction([new Literal(“r”, [“y”,”z”], false)]) ])

Semantics of Objects, Entities and Locations

  • The semantics of an object description is a collection of
    the objects that match the description:

    • type ObjectSemantics = string[]
    • Example: the semantics of “large box” is ["RedBox", "YellowBox"]

  • The semantics of an Entity or a Location is just a wrapper
    around the semantics of its children:

    • type EntitySemantics = {quantifier : string; object : ObjectSemantics}
    • type LocationSemantics = {relation : string; entity : EntitySemantics}
    • Example: the semantics of “in every large box” is
      {relation: "inside", {quantifier: "all", object: ["RedBox", "YellowBox"]}}

Semantic ambiguity

  • DNF inherently captures ambiguity

    • “put a ball in a box”
      \(\Rightarrow\)
      inside(WhiteBall,RedBox) ∨ inside(WhiteBall,YellowBox) ∨ inside(BlackBall,RedBox) ∨ inside(BlackBall,YellowBox) ∨ inside(BlackBall,BlueBox)

  • But impossible interperetations should be removed

    • Note that we don’t want the interpretation inside(WhiteBall,BlueBox),
      because that violates the physical laws.

Only keep valid interpretations

“put the white ball in a box on the floor”

  • “put the white ball in a box that is on the floor” \(\Rightarrow\) inside(WhiteBall,YellowBox)
  • “put the white ball that is in a box on the floor” \(\Rightarrow\) There is no white ball in a box

“in a box on the floor”: Natural interpretation

inside(WhiteBall, YellowBox)
The yellow box is already on the floor: 17 actions to complete

  •  

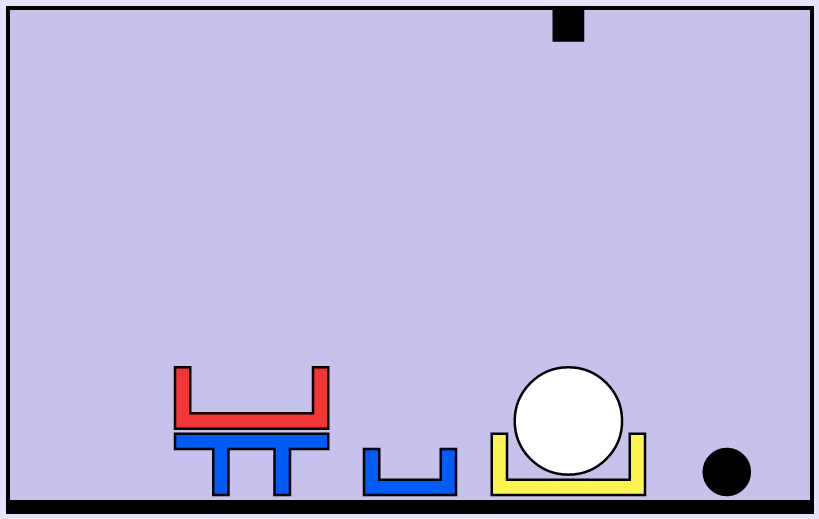
“in a box on the floor”: Alternative interpretation

inside(WhiteBall, RedBox) ∧ on(RedBox, floor)
The red box can be placed on the floor first: 10 actions to complete

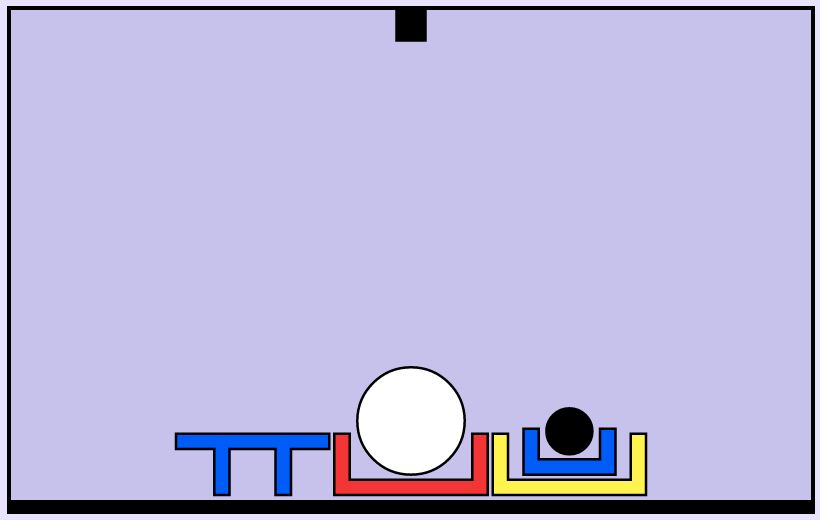
  • The red box is not on the floor at the start!

Final interpretation

“put the white ball in a box on the floor”


So, what should the final interpretation be?

  • inside(WhiteBall, YellowBox)
  • inside(WhiteBall, YellowBox) ∨ (inside(WhiteBall, RedBox) ∧ on(RedBox, floor))

More complex semantic ambiguity

  • “put a ball right of a box in a box beside a table”

  • Which object (i.e., which ball) should be placed
    where (i.e., beside or in which box, or beside
    which table)?

  • I.e., what should the goal be for each of
    the syntactic analyses?

  • “put (a ball) right of ((a box in a box) beside a table)”
  • “put (a ball) right of (a box in (a box beside a table))”
  • “put (a ball right of a box) in (a box beside a table)”
  • “put ((a ball right of a box) in a box) beside (a table)”
  • “put (a ball right of (a box in a box)) beside (a table)”

Physical laws

  • These are the physical laws that the interpreter and planner must check for:

    • The floor can support at most N objects (beside each other).
    • All objects must be supported by something.
    • The arm can only hold one object at the time.
    • The arm can only pick up free objects.
    • Objects are “inside” boxes, but “ontop” of other objects.
    • Balls must be in boxes or on the floor, otherwise they roll away.
    • Balls cannot support anything.
    • Small objects cannot support large objects.
    • Boxes cannot contain pyramids, planks or boxes of the same size.
    • Small boxes cannot be supported by small bricks or pyramids.
    • Large boxes cannot be supported by large pyramids.

Interpreter test cases

  • Each test case contains a list of interpretations, each interpretation is a string
    (a compact representation of a disjunction of conjunctions)

    • if one parse gives several interpretations:

  • world: "small", utterance: "take a blue object" interpretations: ["holding(BlueTable) | holding(BlueBox)"]

    • if several parses give interpretations:

  • world: "small" utterance: "put a black ball in a box on the floor" interpretations: ["inside(BlackBall, YellowBox)", "ontop(BlackBall, floor)"]

Test cases: Conjunctions and invalid utterances

  •  

    • The “all” quantifier gives rise to a conjunction:

  • world: "small" utterance: "put all balls on the floor" interpretations: ["ontop(WhiteBall, floor) & ontop(BlackBall, floor)"]

    • If an utterance breaks the laws of nature:

  • world: "small" utterance: "put a ball on a table" interpretations: []

Test cases: Missing interpretations

  •  
    • There are some cases where the interpretation is missing:

  • world: "small" utterance: "put a ball in a box on the floor" interpretations: ["COME-UP-WITH-YOUR-OWN-INTERPRETATION"]

  • You should discuss these cases in your group and come up with
    good interpretations!