Chapters 4–5: Non-classical and adversarial search

DIT411/TIN175, Artificial Intelligence

Peter Ljunglöf

2 February, 2018

Table of contents

Repetition

Uninformed search (R&N 3.4)

  • Search problems, graphs, states, arcs, goal test, generic search algorithm, tree search, graph search, depth-first search, breadth-first search, uniform cost search, iterative deepending, bidirectional search, …
 

Heuristic search (R&N 3.5–3.6)

  • Greedy best-first search, A* search, heuristics, admissibility, consistency, dominating heuristics, …
 

Local search (R&N 4.1)

  • Hill climbing / gradient descent, random moves, random restarts, beam search, simulated annealing, …

Non-classical search

Nondeterministic search (R&N 4.3)

Partial observations (R&N 4.4)

Nondeterministic search (R&N 4.3)

    • Contingency plan / strategy
    • And-or search trees (not in the written exam)

An erratic vacuum cleaner

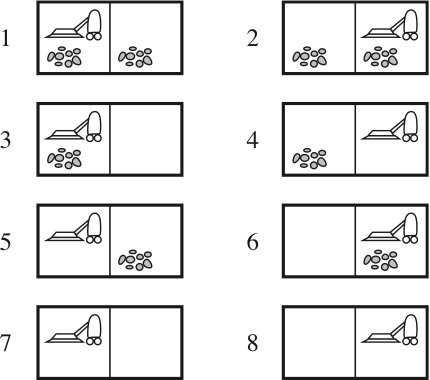
  • The eight possible states of the vacuum world; states 7 and 8 are goal states.

  • There are three actions: Left, Right, Suck.
    Assume that the Suck action works as follows:

    • if the square is dirty, it is cleaned but sometimes also the adjacent square is
    • if the square is clean, the vacuum cleaner sometimes deposists dirt

Nondeterministic outcomes, contingency plans

  • Assume that the Suck action is nondeterministic:
    • if the square is dirty, it is cleaned but sometimes also the adjacent square is
    • if the square is clean, the vacuum cleaner sometimes deposists dirt
  •  
  • Now we need a more general result function:
    • instead of returning a single state, it returns a set of possible outcome states
    • e.g., \(\textsf{Results}(\textsf{Suck}, 1) = \{5, 7\}\) and  \(\textsf{Results}(\textsf{Suck}, 5) = \{1, 5\}\)
  •  
  • We also need to generalise the notion of a solution:
    • instead of a single sequence (path) from the start to the goal,
      we need a strategy (or a contingency plan)
    • i.e., we need if-then-else constructs
    • this is a possible solution from state 1:
      • [Suck, if State=5 then [Right, Suck] else []]

How to find contingency plans

(will not be in the written examination)

  • We need a new kind of nodes in the search tree:
    • and nodes:
      these are used whenever an action is nondeterministic
    • normal nodes are called or nodes:
      they are used when we have several possible actions in a state
  •  
  • A solution for an and-or search problem is a subtree that:
    • has a goal node at every leaf
    • specifies exactly one action at each of its or node
    • includes every branch at each of its and node

A solution to the erratic vacuum cleaner

(will not be in the written examination)

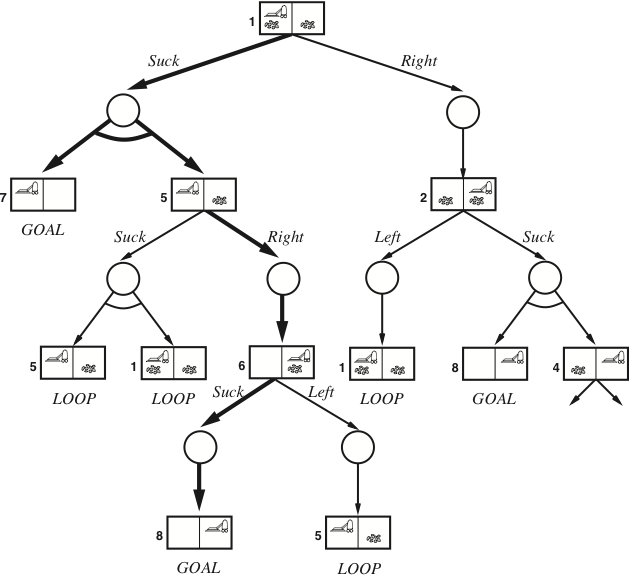
The solution subtree is shown in bold, and corresponds to the plan:
[Suck, if State=5 then [Right, Suck] else []]

An algorithm for finding a contingency plan

(will not be in the written examination)

This algorithm does a depth-first search in the and-or tree,
so it is not guaranteed to find the best or shortest plan:

  • function AndOrGraphSearch(problem):
    • return OrSearch(problem.InitialState, problem, [])
  •  
  • function OrSearch(state, problem, path):
    • if problem.GoalTest(state) then return []
    • if state is on path then return failure
    • for each action in problem.Actions(state):
      • plan := AndSearch(problem.Results(state, action), problem, [state] ++ path)
      • if plan ≠ failure then return [action] ++ plan
    • return failure
  •  
  • function AndSearch(states, problem, path):
    • for each \(s_i\) in states:
      • \(plan_i\) := OrSearch(\(s_i\), problem, path)
      • if \(plan_i\) = failure then return failure
    • return [if \(s_1\) then \(plan_1\) else if \(s_2\) then \(plan_2\) else … if \(s_n\) then \(plan_n\)]

While loops in contingency plans

(will not be in the written examination)

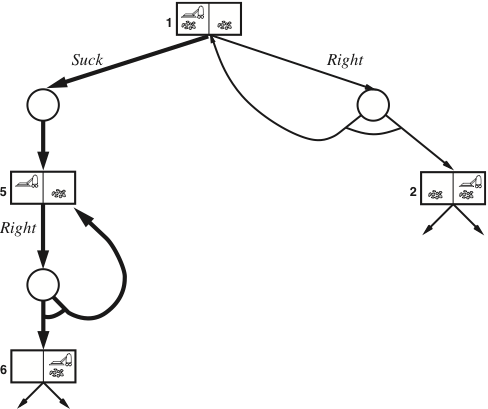
  • If the search graph contains cycles, if-then-else is not enough in a contingency plan:
    • we need while loops instead
  •  
  • In the slippery vacuum world above, the cleaner don’t always move when told:
    • the solution above translates to [Suck, while State=5 do Right, Suck]

Partial observations (R&N 4.4)

    • Belief states: goal test, transitions, …
    • Sensor-less (conformant) problems
    • Partially observable problems

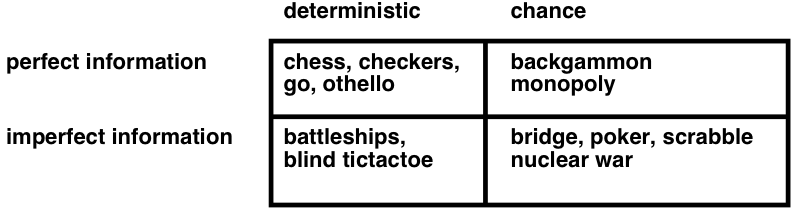
Observability vs determinism

  • A problem is nondeterministic if there are several possible outcomes of an action
    • deterministic — nondeterministic (chance)
  •  
  • It is partially observable if the agent cannot tell exactly which state it is in
    • fully observable (perfect info.) — partially observable (imperfect info.)
  •  
  • A problem can be either nondeterministic, or partially observable, or both:

Belief states

  • Instead of searching in a graph of states, we use belief states
    • A belief state is a set of states
  •  
  • In a sensor-less (or conformant) problem, the agent has no information at all
    • The initial belief state is the set of all problem states
      • e.g., for the vacuum world the initial state is {1,2,3,4,5,6,7,8}
  •  
  • The goal test has to check that all members in the belief state is a goal
    • e.g., for the vacuum world, the following are goal states: {7}, {8}, and {7,8}
  •  
  • The result of performing an action is the union of all possible results
    • i.e., \(\textsf{Predict}(b,a) = \{\textsf{Result}(s,a)\) for each \(s\in b\}\)
    • if the problem is also nondeterministic:
      • \(\textsf{Predict}(b,a) = \bigcup\{\textsf{Results}(s,a)\) for each \(s\in b\}\)

Predicting belief states in the vacuum world

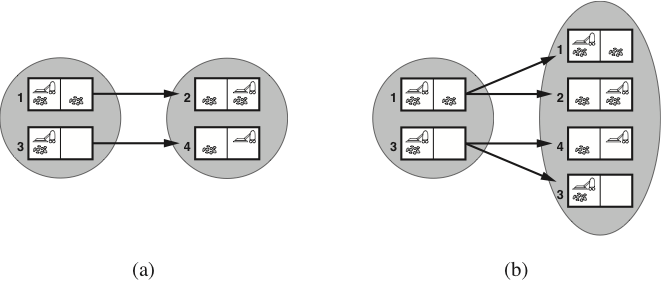
  • (a) Predicting the next belief state for the sensorless vacuum world
    with a deterministic action, Right.

  • (b) Prediction for the same belief state and action in the nondeterministic
    slippery version of the sensorless vacuum world.

The deterministic sensorless vacuum world

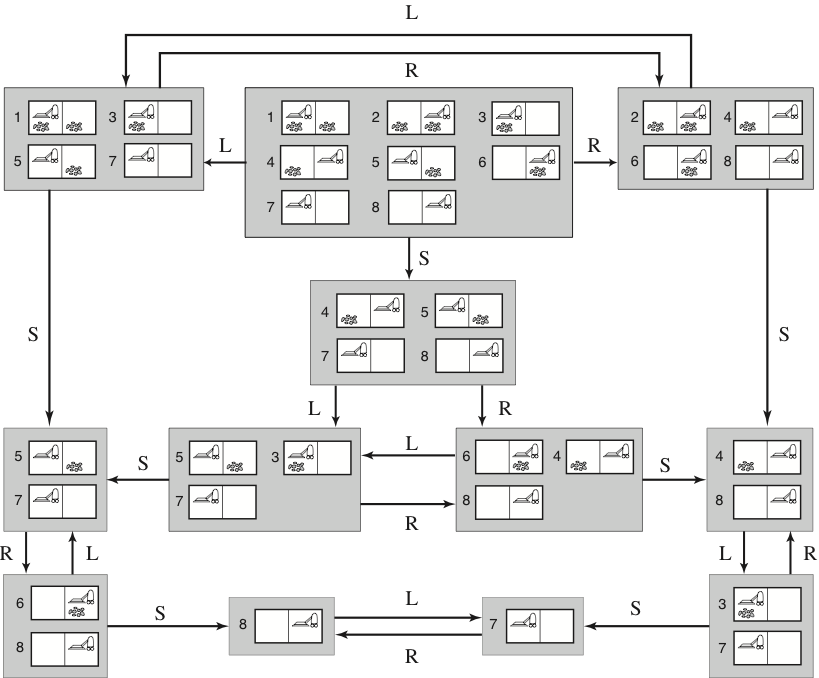
Partial observations: state transitions

  • With partial observations, we can think of belief state transitions in three stages:
    • Prediction, the same as for sensorless problems:
      • \(b’ = \textsf{Predict}(b,a) = \{\textsf{Result}(s,a)\) for each \(s\in b\}\)
    • Observation prediction, determines the percepts that can be observed:
      • \(\textsf{PossiblePercepts}(b’) = \{\textsf{Percept}(s)\) for each \(s\in b’\}\)
    • Update, filters the predicted states according to the percepts:
      • \(\textsf{Update}(b’,o) = \{s\) for each \(s\in b’\) such that \(o = \textsf{Percept}(s)\}\)
  •  
  • Belief state transitions:
    • \(\textsf{Results}(b,a) = \{\textsf{Update}(b’,o)\) for each \(o\in\textsf{PossiblePercepts}(b’)\}\)
      where   \(b’ = \textsf{Predict}(b,a)\)

Transitions in partially observable vacuum worlds

  • The percepts return the current position and the dirtyness of that square.
  •  
  •  
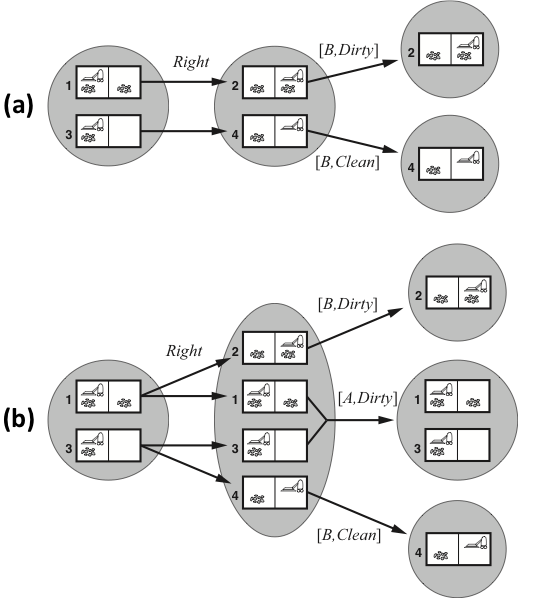
  • The deterministic world:
    Right always succeeds.
  •  
  •  
  •  
  •  
  •  
  •  
  • The slippery world:
    Right sometimes fails.

Example: Robot Localisation

The percepts return whether there is a wall in each of the directions.

  • Possible initial positions of the robot, after E1 = North, South, West.

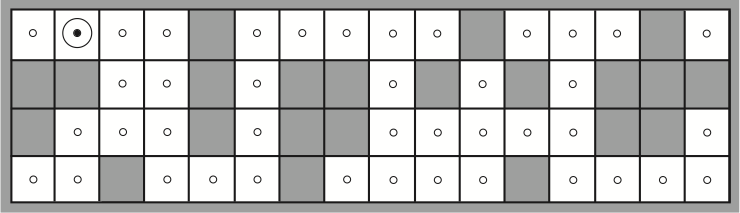
  • After moving right and observing E2 = North, South,
    there’s only one possible position left.

Adversarial search

Types of games (R&N 5.1)

Minimax search (R&N 5.2–5.3)

Imperfect decisions (R&N 5.4–5.4.2)

Stochastic games (R&N 5.5)

Types of games (R&N 5.1)

    • cooperative, competetive, zero-sum games
    • game trees, ply/plies, utility functions

Multiple agents

  • Let’s consider problems with multiple agents, where:

    • the agents select actions autonomously

    • each agent has its own information state
      • they can have different information (even conflicting)

    • the outcome depends on the actions of all agents

    • each agent has its own utility function (that depends on the total outcome)

Types of agents

  • There are two extremes of multiagent systems:

    • Cooperative: The agents share the same utility function
      • Example: Automatic trucks in a warehouse
    • Competetive: When one agent wins all other agents lose
      • A common special case is when \(\sum_{a}u_{a}(o)=0\) for any outcome \(o\).
        This is called a zero-sum game.
      • Example: Most board games

  • Many multiagent systems are between these two extremes.

    • Example: Long-distance bike races are usually both cooperative
      (bikers form clusters where they take turns in leading a group),
      and competetive (only one of them can win in the end).

Games as search problems

  • The main difference to chapters 3–4:
    now we have more than one agent that have different goals.

    • All possible game sequences are represented in a game tree.

    • The nodes are states of the game, e.g. board positions in chess.

    • Initial state (root) and terminal nodes (leaves).

    • States are connected if there is a legal move/ply.
      (a ply is a move by one player, i.e., one layer in the game tree)

    • Utility function (payoff function). Terminal nodes have utility values
      \({+}x\) (player 1 wins), \({-}x\) (player 2 wins) and \(0\) (draw).

Types of games (again)

Perfect information games: Zero-sum games

  • Perfect information games are solvable in a manner similar to
    fully observable single-agent systems, e.g., using forward search.

  • If two agents compete, so that a positive reward for one is a negative reward
    for the other agent, we have a two-agent zero-sum game.

  • The value of a game zero-sum game can be characterised by a single number that one agent is trying to maximise and the other agent is trying to minimise.

  • This leads to a minimax strategy:

    • A node is either a MAX node (if it is controlled by the maximising agent),
    • or is a MIN node (if it is controlled by the minimising agent).

Minimax search (R&N 5.2–5.3)

    • Minimax algorithm
    • α-β pruning

Minimax search for zero-sum games

  • Given two players called MAX and MIN:
    • MAX wants to maximise the utility value,
    • MIN wants to minimise the same value.
  • \(\Rightarrow\) MAX should choose the alternative that maximises, assuming MIN minimises.
  •  
  • Minimax gives perfect play for deterministic, perfect-information games:
 
  • function Minimax(state):
    • if TerminalTest(state) then return Utility(state)
    • A := Actions(state)
    • if state is a MAX node then return \(\max_{a\in A}\) Minimax(Result(state, a))
    • if state is a MIN node then return \(\min_{a\in A}\) Minimax(Result(state, a))

Minimax search: tic-tac-toe

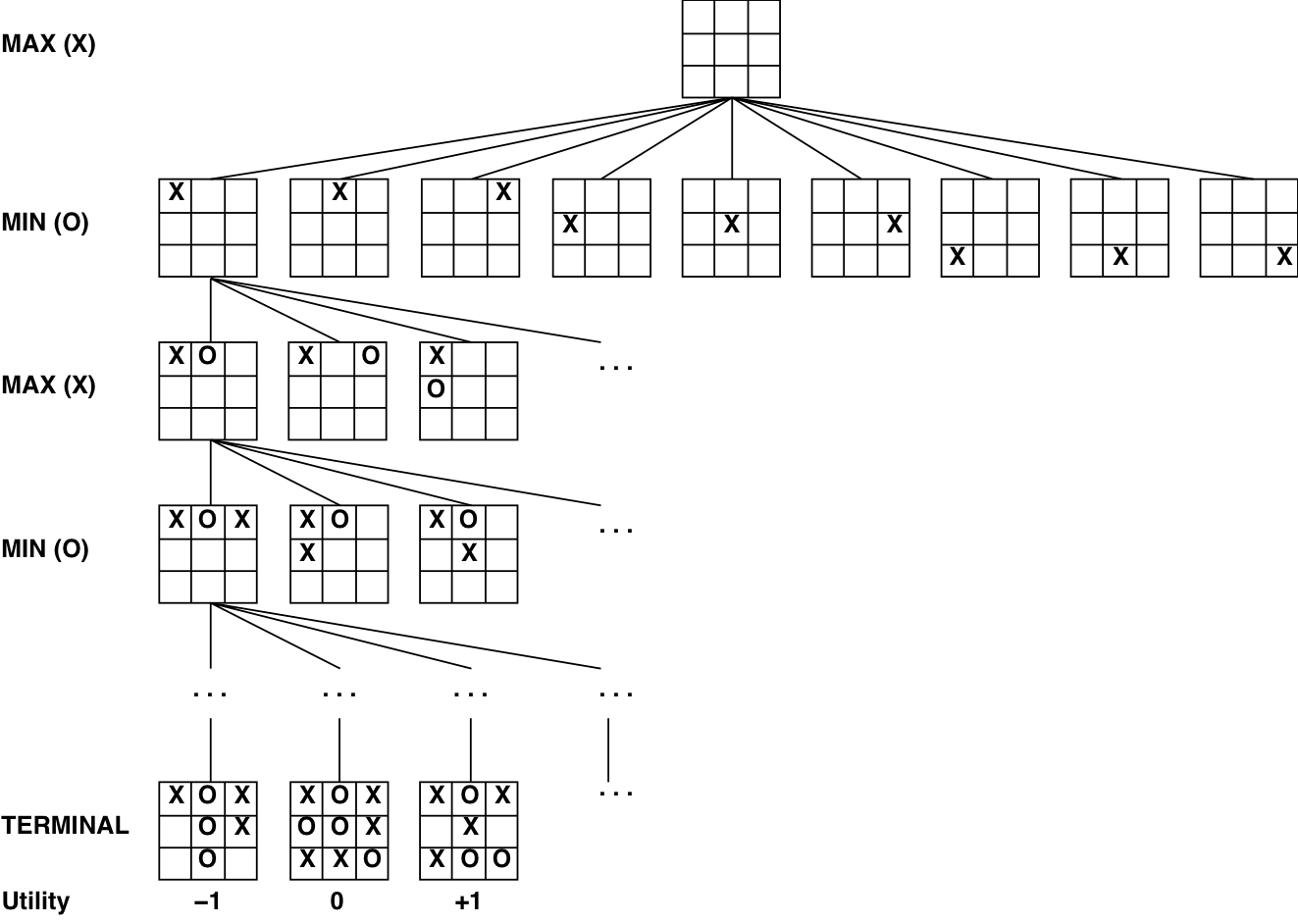
Minimax example

The Minimax algorithm gives perfect play for deterministic, perfect-information games.

Can Minimax be wrong?

  • Minimax gives perfect play, but is that always the best strategy?

  • Perfect play assumes that the opponent is also a perfect player!

3-player minimax

(will not be in the written examination)

Minimax can also be used on multiplayer games

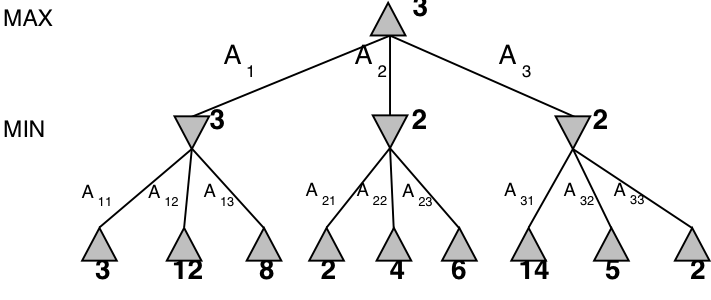
\(\alpha{-}\beta\,\) pruning

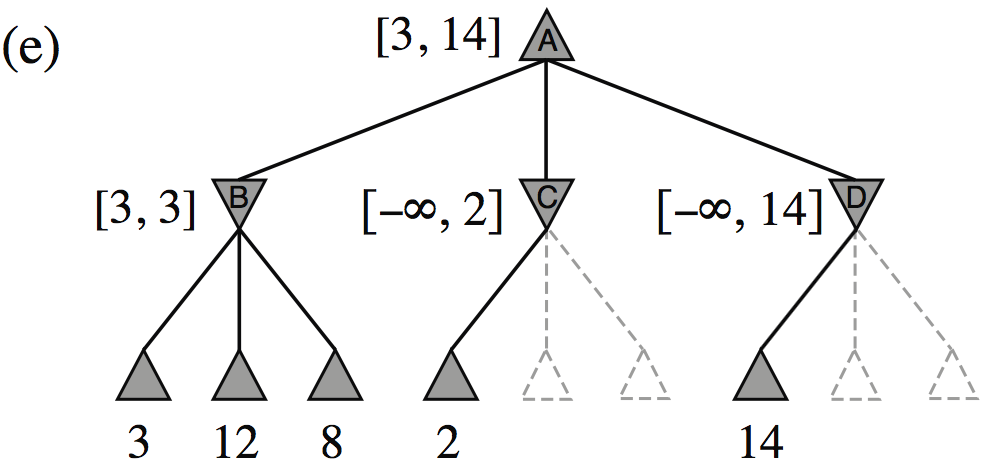
Minimax(root) = \( \max(\min(3,12,8), \min(2,x,y), \min(14,5,2)) \)
  = \( \max(3, \min(2,x,y), 2) \)
  = \( \max(3, z, 2) \)   where  \(z = \min(2,x,y) \leq 2\)
  = \( 3 \)
  • I.e., we don’t need to know the values of \(x\) and \(y\)!

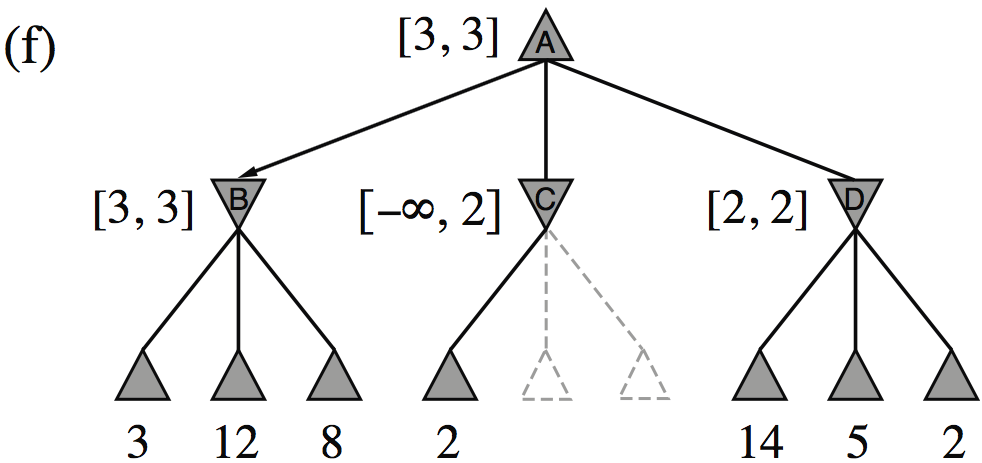
\(\alpha{-}\beta\,\) pruning, general idea

  •  
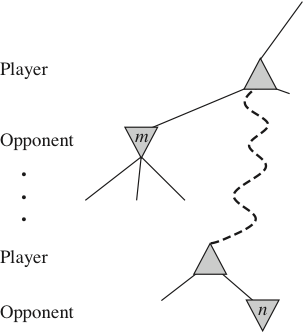
  • The general idea of α-β pruning is this:
  •   •  if \(m\) is better than \(n\) for Player,
  •      we don’t want to pursue \(n\)
  •   •  so, once we know enough about \(n\)
  •      we can prune it
  •   •  sometimes it’s enough to examine
  •      just one of \(n\)’s descendants
  •  
  •  
  •  
  • α-β pruning keeps track of the possible range of values for every node it visits;
    the parent range is updated when the child has been visited.

Minimax example, with \(\alpha{-}\beta\) pruning

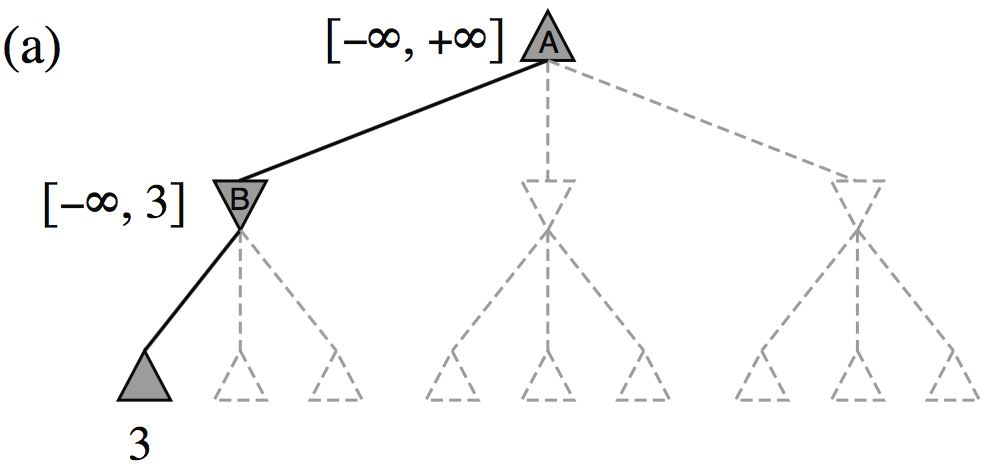
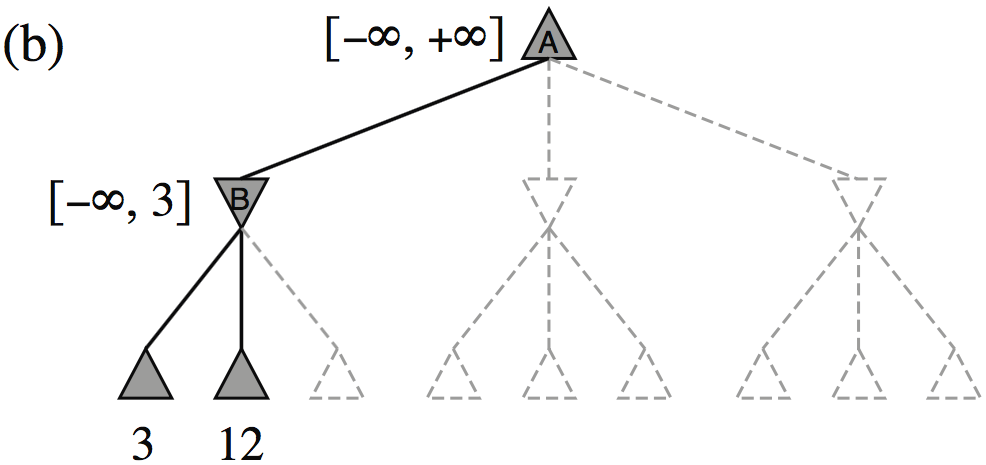
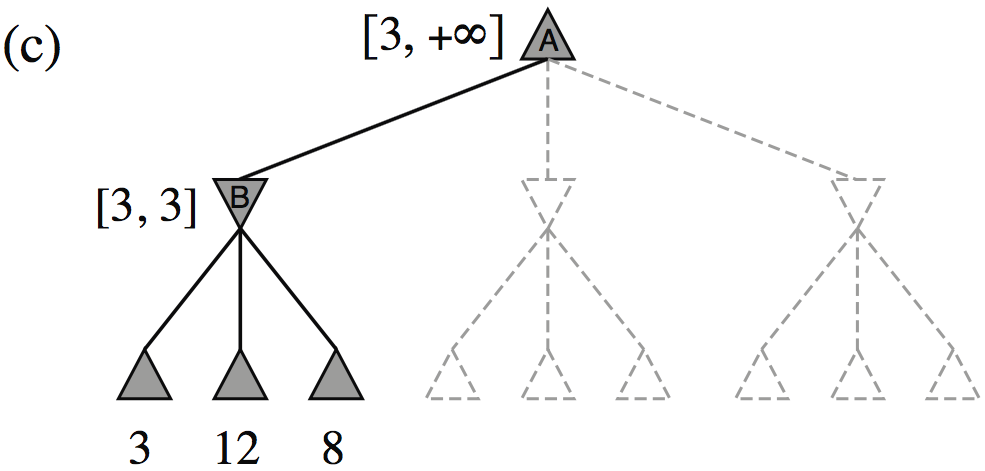
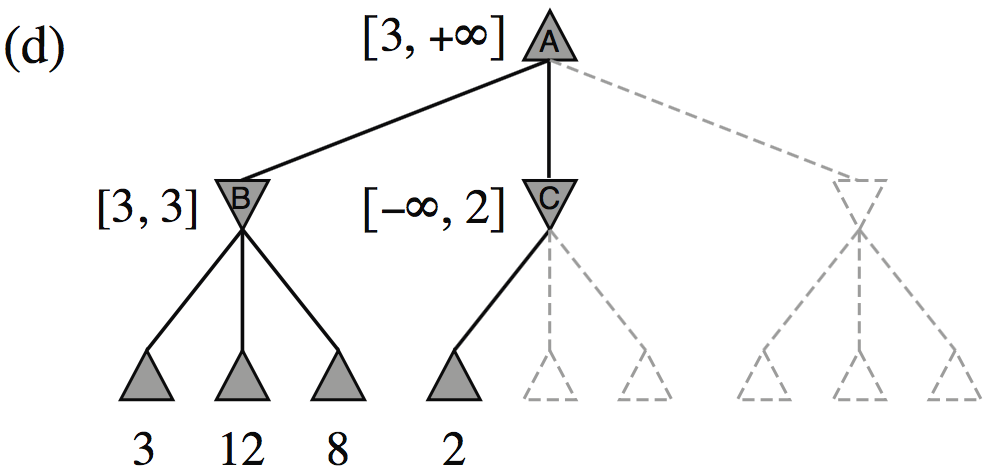
The \(\alpha{-}\beta\) algorithm

  • function AlphaBetaSearch(state):
    • v := MaxValue(state, \(-\infty\), \(+\infty\)))
    • return the action in Actions(state) that has value v
  •  
  • function MaxValue(state, α, β):
    • if TerminalTest(state) then return Utility(state)
    • v := \(-\infty\)
    • for each action in Actions(state):
      • v := max(v, MinValue(Result(state, action), α, β))
      • if v ≥ β then return v
      • α := max(α, v)
    • return v
  •  
  • function MinValue(state, α, β):
    • same as MaxValue but reverse the roles of α/β and min/max and \(-\infty/{+}\infty\)

How efficient is \(\alpha{-}\beta\) pruning?

  • The amount of pruning provided by the α-β algorithm depends on the ordering of the children of each node.

    • It works best if a highest-valued child of a MAX node is selected first and
      if a lowest-valued child of a MIN node is selected first.

    • In real games, much of the effort is made to optimise the search order.

    • With a “perfect ordering”, the time complexity becomes \(O(b^{m/2})\)

      • this doubles the solvable search depth
      • however, \(35^{80/2}\) (for chess) or \(250^{160/2}\) (for go) is still quite large…

Minimax and real games

  • Most real games are too big to carry out minimax search, even with α-β pruning.

    • For these games, instead of stopping at leaf nodes,
      we have to use a cutoff test to decide when to stop.

    • The value returned at the node where the algorithm stops
      is an estimate of the value for this node.

    • The function used to estimate the value is an evaluation function.

    • Much work goes into finding good evaluation functions.

    • There is a trade-off between the amount of computation required
      to compute the evaluation function and the size of the search space
      that can be explored in any given time.

Imperfect decisions (R&N 5.4–5.4.2)

    • H-minimax algorithm
    • evaluation function, cutoff test
    • features, weighted linear function
    • quiescence search, horizon effect

H-minimax algorithm

  • The Heuristic Minimax algorithm is similar to normal Minimax
    • it replaces TerminalTest with CutoffTest, and Utility with Eval
    • the cutoff test needs to know the current search depth
 
  • function H-Minimax(state, depth):
    • if CutoffTest(state, depth) then return Eval(state)
    • A := Actions(state)
    • if state is a MAX node then return \(\max_{a\in A}\) H-Minimax(Result(state, a), depth+1)
    • if state is a MIN node then return \(\min_{a\in A}\) H-Minimax(Result(state, a), depth+1)

Chess positions: how to evaluate

Weighted linear evaluation functions

  • A very common evaluation function is to use a weighted sum of features: \[ Eval(s) = w_1 f_1(s) + w_2 f_2(s) + \cdots + w_n f_n(s) = \sum_{i=1}^{n} w_i f_i(s) \]

  • This relies on a strong assumption: all features are independent of each other
    • which is usually not true, so the best programs for chess
      (and other games) also use nonlinear feature combinations
  •  
  • The weights can be calculated using machine learning algorithms,
    but a human still has to come up with the features.
    • using recent advances in deep machine learning,
      the computer can learn the features too

Evaluation functions

A naive weighted sum of features will not see the difference between these two states.

Problems with cutoff tests

  • Too simplistic cutoff tests and evaluation functions can be problematic:
    • e.g., if the cutoff is only based on the current depth
    • then it might cut off the search in unfortunate positions
      (such as (b) on the previous slide)
  •  
  • We want more sophisticated cutoff tests:
    • only cut off search in quiescent positions
    • i.e., in positions that are “stable”, unlikely to exhibit wild swings in value
    • non-quiescent positions should be expanded further
  •  
  • Another problem is the horizon effect:
    • if a bad position is unavoidable (e.g., loss of a piece), but the system can
      delay it from happening, it might push the bad position “over the horizon”
    • in the end, the resulting delayed position might be even worse

Deterministic games in practice

  • Chess:
    • IBM DeepBlue beats world champion Garry Kasparov, 1997.
    • Google AlphaZero beats best chess program Stockfish, December 2017.
  •  
  • Checkers/Othello/Reversi:
    • Logistello beats the world champion in Othello/Reversi, 1997.
    • Chinook plays checkers perfectly, 2007. It uses an endgame database
      defining perfect play for all 8-piece positions on the board,
      (a total of 443,748,401,247 positions).
  •  
  • Go:
    • First Go programs to reach low dan-levels, 2009.
    • Google AlphaGo beats the world’s best Go player, Ke Jie, May 2017.
    • Google AlphaZero beats AlphaGo, December 2017.
      • AlphaZero learns board game strategies by playing itself, it does not use a database of previous matches, opening books or endgame tables.

Stochastic games (R&N 5.5)

Note: this section will be presented Tuesday 6th February!