Chapters 3, 4, 5, 7: Repetition

DIT411/TIN175, Artificial Intelligence

Peter Ljunglöf

9 February, 2018

Table of contents

Search (R&N 3.1–3.6, 4.1, 4.3–4.4)

Heuristics

Directed Graphs

  • A graph consists of a set \(N\) of nodes and a set \(A\) of ordered pairs of nodes,
    called arcs or edges.

    • Node \(n_2\) is a neighbor of \(n_1\) if there is an arc from \(n_1\) to \(n_2\).
      That is, if \( (n_1, n_2) \in A \).

    • A path is a sequence of nodes \( (n_0, n_1, \ldots, n_k) \) such that \( (n_{i-1}, n_i) \in A \).

    • The length of path \( (n_0, n_1, \ldots, n_k) \) is \(k\).

    • A solution is a path from a start node to a goal node,
      given a set of start nodes and goal nodes.

    • (Russel & Norvig sometimes call the graph nodes states).

How do we search in a graph?

  • A generic search algorithm:

    • Given a graph, start nodes, and a goal description, incrementally
      explore paths from the start nodes.

    • Maintain a frontier of nodes that are to be explored.

    • As search proceeds, the frontier expands into the unexplored nodes
      until a goal node is encountered.

    • The way in which the frontier is expanded defines the search strategy.

Illustration of searching in a graph

The generic tree search algorithm

  • Tree search: Don’t check if nodes are visited multiple times
 
  • function Search(graph, initialState, goalState):
    • initialise frontier using the initialState
    •  
    • while frontier is not empty:
      • select and remove node from frontier
      • if node.state is a goalState then return node
      •  
      • for each child in ExpandChildNodes(node, graph):
        • add child to frontier
    • return failure

Using tree search on a graph

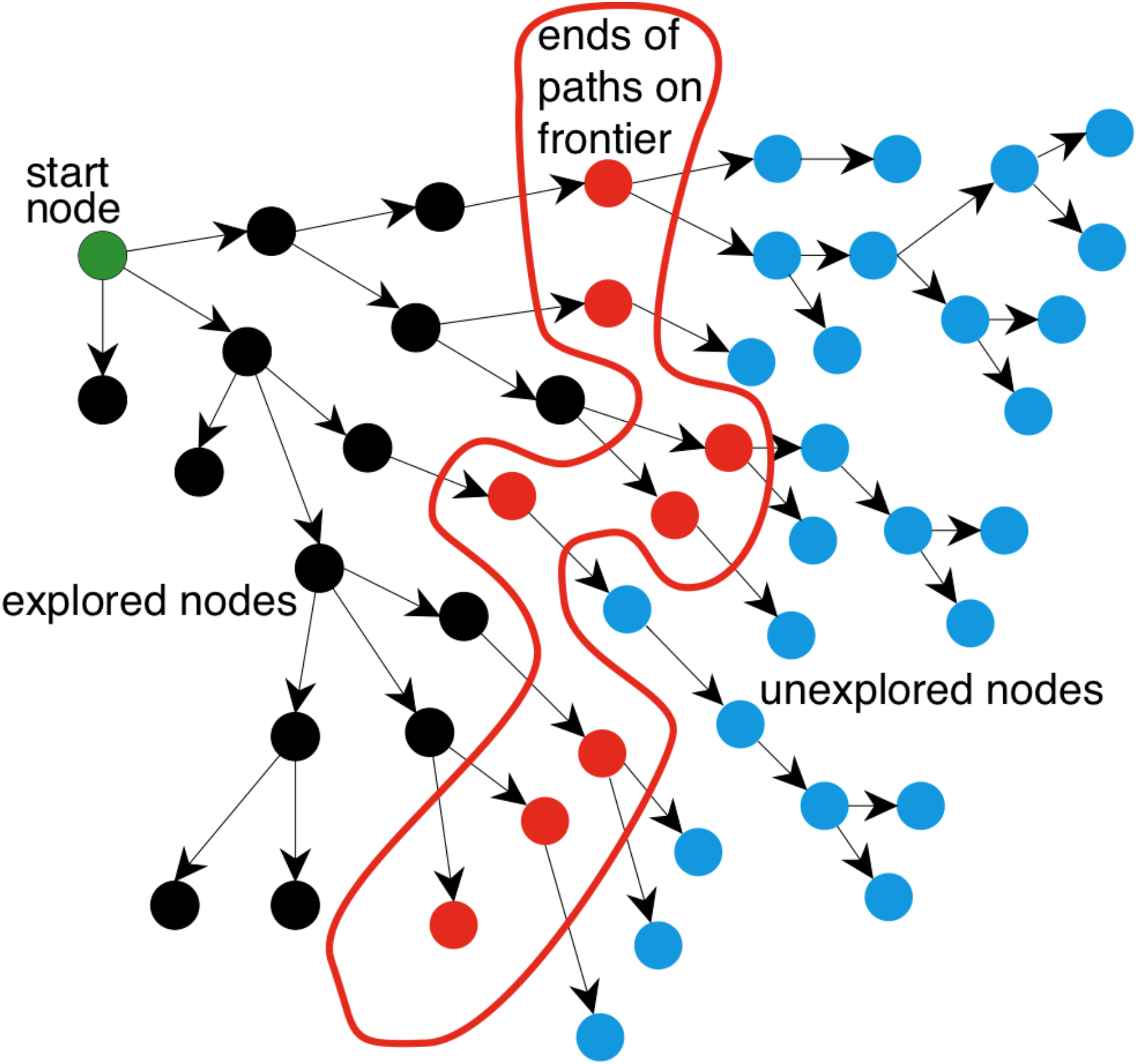
    • explored nodes might be revisited
    • frontier nodes might be duplicated
  • Graph search: Keep track of visited nodes
 
  • function Search(graph, initialState, goalState):
    • initialise frontier using the initialState
    • initialise exploredSet to the empty set
    • while frontier is not empty:
      • select and remove node from frontier
      • if node.state is a goalState then return node
      • add node to exploredSet
      • for each child in ExpandChildNodes(node, graph):
        • add child to frontier if child is not in frontier or exploredSet
    • return failure

  • Tree search

    • Pro: uses less memory
    • Con: might visit the same node several times

  • Graph search

    • Pro: only visits nodes at most once
    • Con: uses more memory

These are the two basic search algorithms

  • Depth-first search (DFS)
    • implement the frontier as a Stack
    • space complexity: \( O(bm) \)
    • incomplete: might fall into an infinite loop, doesn’t return optimal solution
  •  
  • Breadth-first search (BFS)
    • implement the frontier as a Queue
    • space complexity: \( O(b^m) \)
    • complete: always finds a solution, if there is one
    • (when edge costs are constant, BFS is also optimal)

Iterative deepening

  • Problems with BFS and DFS:

    • BFS is guaranteed to halt but uses exponential space.
    • DFS uses linear space, but is not guaranteed to halt.

  • Idea: take the best from BFS and DFS — recompute elements of the frontier
    rather than saving them.

    • Look for paths of depth 0, then 1, then 2, then 3, etc.
    • Depth-bounded DFS can do this in linear space.

  • Iterative deepening search calls depth-bounded DFS with increasing bounds:

    • If a path cannot be found at depth-bound, look for a path at depth-bound + 1.
    • Increase depth-bound when the search fails unnaturally
      (i.e., if depth-bound was reached).

Iterative deepening complexity

Complexity with solution at depth \(k\) and branching factor \(b\):

level # nodes BFS node visits ID node visits
\(1\)
\(2\)
\(3\)
\(\vdots\)
\(k\)		 \(b\)
\(b^{2}\)
\(b^{3}\)
\(\vdots\)
\(b^{k}\)		 \(1\cdot b^{1}\)
\(1\cdot b^{2}\)
\(1\cdot b^{3}\)
\(\vdots\)
\(1\cdot b^{k}\)		 \(\,\,\,\,\,\,\,\,k\,\,\cdot b^{1}\)
\((k{-}1)\cdot b^{2}\)
\((k{-}2)\cdot b^{3}\)
\(\,\,\,\,\,\,\,\,\vdots\)
\(\,\,\,\,\,\,\,\,1\,\,\cdot b^{k}\)
total   \({}\geq b^{k}\) \({}\leq b^{k}\left(\frac{b}{b-1}\right)^{2}\)

Numerical comparison for \(k=5\) and \(b=10\):

  • BFS  =  10 + 100 + 1,000 + 10,000 + 100,000  =  111,110
  • IDS   =  50 + 400 + 3,000 + 20,000 + 100,000  =  123,450

Note: IDS recalculates shallow nodes several times,
but this doesn’t have a big effect compared to BFS!

(will not be in the written examination, but could be used in Shrdlite)

  • Idea: search backward from the goal and forward from the start simultaneously.

    • This can result in an exponential saving, because \(2b^{k/2}\ll b^{k}\).

    • The main problem is making sure the frontiers meet.

  • One possible implementation:

    • Use BFS to gradually search backwards from the goal,
      building a set of locations that will lead to the goal.

      • this can be done using dynamic programming

    • Interleave this with forward heuristic search (e.g., A*)
      that tries to find a path to these interesting locations.

Cost-based search

The frontier is a Priority Queue, ordered by \(f(n)\)

  • Uniform-cost search (this is not a heuristic algorithm)
    • expand the node with the lowest path cost
    • \( f(n) = g(n) \)
    • complete and optimal
  •  
  • Greedy best-first search
    • expand the node which is closest to the goal (according to some heuristics)
    • \( f(n) = h(n) \)
    • incomplete: might fall into an infinite loop, doesn’t return optimal solution
  •  
  • A* search
    • expand the node which has the lowest estimated cost from start to goal
    • \( f(n) = g(n) + h(n) \) = estimated cost of the cheapest solution through \(n\)
    • complete and optimal (if \(h(n)\) is admissible/consistent)

A* tree search is optimal!

  • A* always finds an optimal solution first, provided that:

    • the branching factor is finite,

    • arc costs are bounded above zero
      (i.e., there is some \(\epsilon>0\) such that all
      of the arc costs are greater than \(\epsilon\)), and

    • \(h(n)\) is admissible

      • i.e., \(h(n)\) is nonnegative and an underestimate of
        the cost of the shortest path from \(n\) to a goal node.

These requirements ensure that \(f\) keeps increasing.

The generic tree search algorithm

Turning tree search into graph search

  • Tree search: Don’t check if nodes are visited multiple times
  • Graph search: Keep track of visited nodes
 
  • function Search(graph, initialState, goalState):
    • initialise frontier using the initialState
    • initialise exploredSet to the empty set
    • while frontier is not empty:
      • select and remove node from frontier
      • if node.state is a goalState then return node
      • add node to exploredSet
      • for each child in ExpandChildNodes(node, graph):
        • add child to frontier if child is not in frontier or exploredSet
    • return failure

Graph-search = Multiple-path pruning

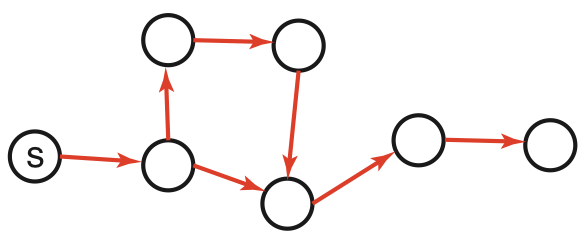
  • Graph search keeps track of visited nodes, so we don’t visit the same node twice.

    • Suppose that the first time we visit a node is not via the most optimal path

            \(\Rightarrow\)   then graph search will return a suboptimal path

    • Under which circumstances can we guarantee that A* graph search is optimal?

When is A* graph search optimal?

  • If  \( |h(n’)-h(n)| \leq cost(n’,n) \)  for every arc  \((n’,n)\),
    then A* graph search is optimal:
  •  
    • Lemma: the \(f\) values along any path \([…,n’,n,…]\) are nondecreasing:
      • Proof: \(g(n) = g(n’) + cost(n’, n)\), therefore:
      • \(f(n) = g(n) + h(n) = g(n’) + cost(n’, n) + h(n) \geq g(n’) + h(n’)\)
      • therefore: \(f(n) \geq f(n’)\), i.e., \(f\) is nondecreasing
  •  
    • Theorem: whenever A* expands a node \(n\), the optimal path to \(n\) has been found
      • Proof: Assume this is not true;
      • then there must be some \(n’\) still on the frontier, which is on the optimal path to \(n\);
      • but \(f(n’) \leq f(n)\);
      • and then \(n’\) must already have been expanded \(\Longrightarrow\) contradiction!

State-space contours

  • The \(f\) values in A* are nondecreasing, therefore:

    first A* expands all nodes with \( f(n) < C \)
    then A* expands all nodes with \( f(n) = C \)
    finally A* expands all nodes with \( f(n) > C \)

  • A* will not expand any nodes with \( f(n) > C* \),
    where \(C*\) is the cost of an optimal solution.

Summary of optimality of A*

  • A* tree search is optimal if:

    • the heuristic function \(h(n)\) is admissible
    • i.e., \(h(n)\) is nonnegative and an underestimate of the actual cost
    • i.e., \( h(n) \leq cost(n,goal) \), for all nodes \(n\)

  • A* graph search is optimal if:

    • the heuristic function \(h(n)\) is consistent (or monotone)
    • i.e., \( |h(m)-h(n)| \leq cost(m,n) \), for all arcs \((m,n)\)

Summary of tree search strategies

Search
strategy		 Frontier
selection		 Halts if solution? Halts if no solution? Space usage
Depth first Last node added No No Linear
Breadth first First node added Yes No Exp
Greedy best first Minimal \(h(n)\) No No Exp
Uniform cost Minimal \(g(n)\) Optimal No Exp
A* \(f(n)=g(n)+h(n)\) Optimal* No Exp


*Provided that \(h(n)\) is admissible.

  • Halts if: If there is a path to a goal, it can find one, even on infinite graphs.
  • Halts if no: Even if there is no solution, it will halt on a finite graph (with cycles).
  • Space: Space complexity as a function of the length of the current path.

Summary of graph search strategies

Search
strategy		 Frontier
selection		 Halts if solution? Halts if no solution? Space usage
Depth first Last node added (Yes)** Yes Exp
Breadth first First node added Yes Yes Exp
Greedy best first Minimal \(h(n)\) (Yes)** Yes Exp
Uniform cost Minimal \(g(n)\) Optimal Yes Exp
A* \(f(n)=g(n)+h(n)\) Optimal* Yes Exp

**On finite graphs with cycles, not infinite graphs.
*Provided that \(h(n)\) is consistent.

  • Halts if: If there is a path to a goal, it can find one, even on infinite graphs.
  • Halts if no: Even if there is no solution, it will halt on a finite graph (with cycles).
  • Space: Space complexity as a function of the length of the current path.

Heuristics

Recapitulation: The 8 puzzle

  • \(h_{1}(n)\) = number of misplaced tiles
  • \(h_{2}(n)\) = total Manhattan distance
    (i.e., no. of squares from desired location of each tile)
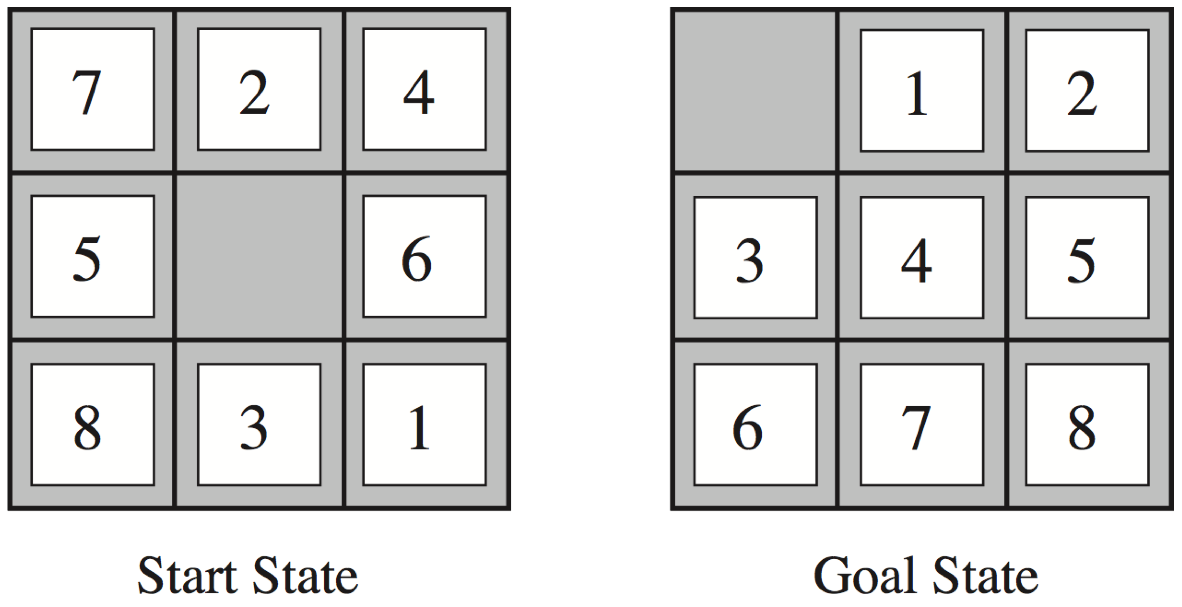
  • \(h_{1}(StartState)\)  =  8
  • \(h_{2}(StartState)\)  =  3+1+2+2+2+3+3+2 = 18

Dominating heuristics

  • If (admissible) \(h_{2}(n)\geq h_{1}(n)\) for all \(n\),
    then \(h_{2}\) dominates \(h_{1}\) and is better for search.

  • Typical search costs (for 8-puzzle):

    depth = 14 DFS  ≈  3,000,000 nodes
    A*(\(h_1\)) = 539 nodes
    A*(\(h_2\)) = 113 nodes
    depth = 24 DFS  ≈  54,000,000,000 nodes
    A*(\(h_1\)) = 39,135 nodes
    A*(\(h_2\)) = 1,641 nodes

  • Given any admissible heuristics \(h_{a}\), \(h_{b}\), the maximum heuristics \(h(n)\)
    is also admissible and dominates both: \[ h(n) = \max(h_{a}(n),h_{b}(n)) \]

Heuristics from a relaxed problem

  • Admissible heuristics can be derived from the exact solution cost of
    a relaxed problem:

    • If the rules of the 8-puzzle are relaxed so that a tile can move anywhere,
      then \(h_{1}(n)\) gives the shortest solution

    • If the rules are relaxed so that a tile can move to any adjacent square,
      then \(h_{2}(n)\) gives the shortest solution

  • Key point: the optimal solution cost of a relaxed problem is
    never greater than the optimal solution cost of the real problem

  • A* search with admissible (consistent) heuristics is optimal

  • But what happens if the heuristics is non-admissible?

    • i.e., what if \(h(n) > c(n,goal)\), for some \(n\)?
    • the solution is not guaranteed to be optimal…
    • …but it will find some solution!

  • Why would we want to use a non-admissible heuristics?

    • sometimes it’s easier to come up with a heuristics that is almost admissible
    • and, often, the search terminates faster!

  •  

  • * for graph search, \( |h(m)-h(n)| > cost(m,n) \), for some \((m,n)\)

Non-classical search

  • A problem is nondeterministic if there are several possible outcomes of an action
    • deterministic — nondeterministic (chance)
  •  
  • It is partially observable if the agent cannot tell exactly which state it is in
    • fully observable (perfect info.) — partially observable (imperfect info.)
  •  
  • A problem can be either nondeterministic, or partially observable, or both:

  • We need a more general result function:
    • instead of returning a single state, it returns a set of possible outcome states
    • e.g., \(\textsf{Results}(\textsf{Suck}, 1) = \{5, 7\}\) and  \(\textsf{Results}(\textsf{Suck}, 5) = \{1, 5\}\)
  •  
  • We also need to generalise the notion of a solution:
    • instead of a single sequence (path) from the start to the goal,
      we need a strategy (or a contingency plan)
    • i.e., we need if-then-else constructs
    • this is a possible solution from state 1:
      • [Suck, if State=5 then [Right, Suck] else []]

How to find contingency plans

(will not be in the written examination)

  • We need a new kind of nodes in the search tree:
    • and nodes:
      these are used whenever an action is nondeterministic
    • normal nodes are called or nodes:
      they are used when we have several possible actions in a state
  •  
  • A solution for an and-or search problem is a subtree that:
    • has a goal node at every leaf
    • specifies exactly one action at each of its or node
    • includes every branch at each of its and node

A solution to the erratic vacuum cleaner

(will not be in the written examination)

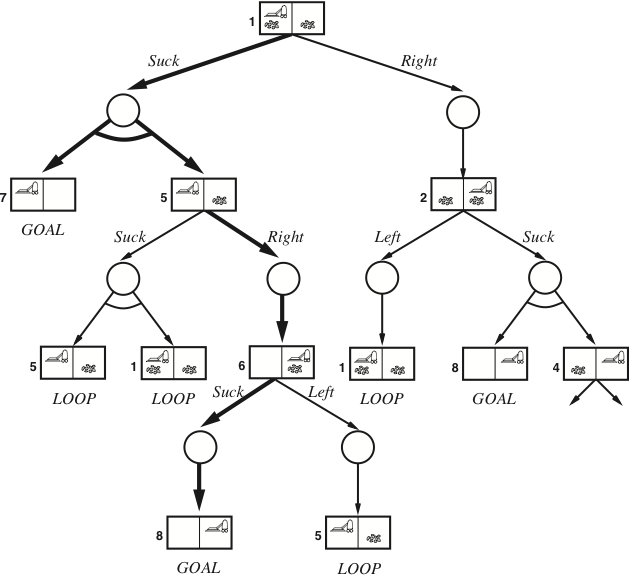
The solution subtree is shown in bold, and corresponds to the plan:
[Suck, if State=5 then [Right, Suck] else []]

Partial observations: Belief states

  • Instead of searching in a graph of states, we use belief states
    • A belief state is a set of states
  •  
  • In a sensor-less (or conformant) problem, the agent has no information at all
    • The initial belief state is the set of all problem states
      • e.g., for the vacuum world the initial state is {1,2,3,4,5,6,7,8}
  •  
  • The goal test has to check that all members in the belief state is a goal
    • e.g., for the vacuum world, the following are goal states: {7}, {8}, and {7,8}
  •  
  • The result of performing an action is the union of all possible results
    • i.e., \(\textsf{Predict}(b,a) = \{\textsf{Result}(s,a)\) for each \(s\in b\}\)
    • if the problem is also nondeterministic:
      • \(\textsf{Predict}(b,a) = \bigcup\{\textsf{Results}(s,a)\) for each \(s\in b\}\)

Predicting belief states in the vacuum world

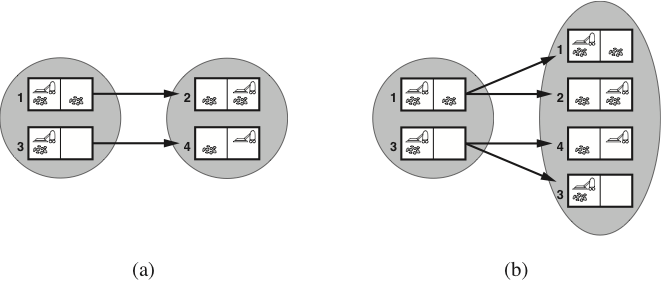
  • (a) Predicting the next belief state for the sensorless vacuum world
    with a deterministic action, Right.

  • (b) Prediction for the same belief state and action in the nondeterministic
    slippery version of the sensorless vacuum world.

Adversarial search (R&N 5.1–5.5)

Types of games

Imperfect decisions

Stochastic games

Games as search problems

  • The main difference to chapters 3–4:
    now we have more than one agent that have different goals.

    • All possible game sequences are represented in a game tree.

    • The nodes are states of the game, e.g. board positions in chess.

    • Initial state (root) and terminal nodes (leaves).

    • States are connected if there is a legal move/ply.
      (a ply is a move by one player, i.e., one layer in the game tree)

    • Utility function (payoff function). Terminal nodes have utility values
      \({+}x\) (player 1 wins), \({-}x\) (player 2 wins) and \(0\) (draw).

Perfect information games: Zero-sum games

  • Perfect information games are solvable in a manner similar to
    fully observable single-agent systems, e.g., using forward search.

  • If two agents compete, so that a positive reward for one is a negative reward
    for the other agent, we have a two-agent zero-sum game.

  • The value of a game zero-sum game can be characterized by a single number that one agent is trying to maximize and the other agent is trying to minimize.

  • This leads to a minimax strategy:

    • A node is either a MAX node (if it is controlled by the maximising agent),
    • or is a MIN node (if it is controlled by the minimising agent).

Minimax search

The Minimax algorithm gives perfect play for deterministic, perfect-information games.

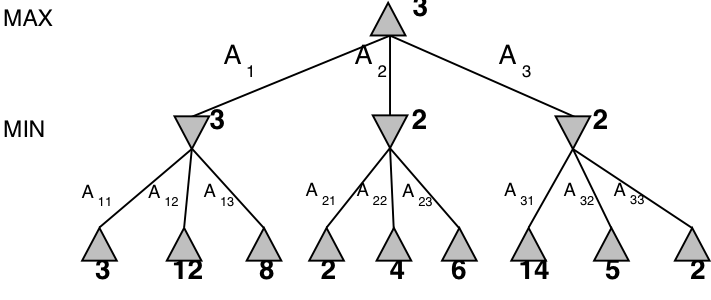
\(\alpha{-}\beta\) pruning

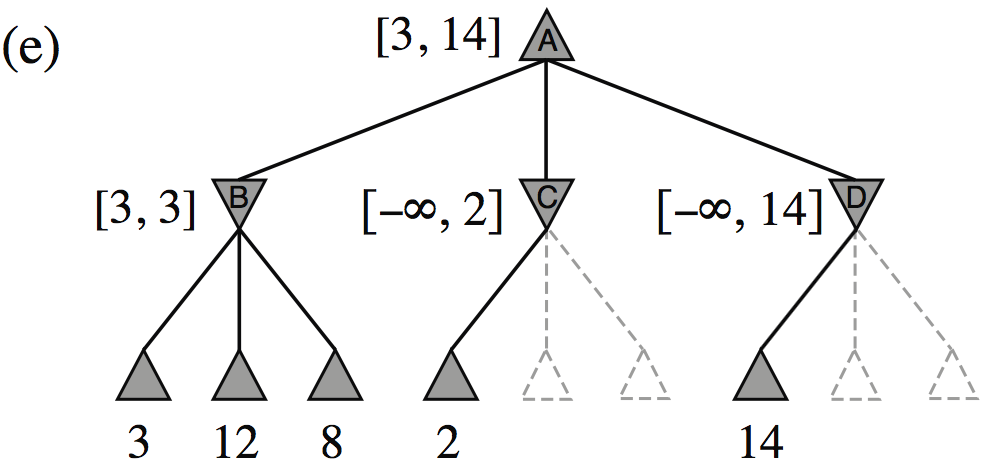
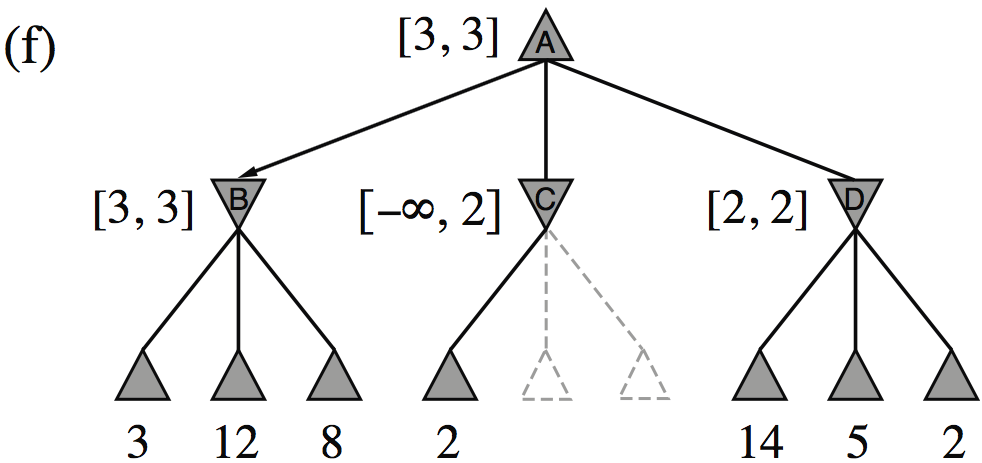
Minimax(root) = \( \max(\min(3,12,8), \min(2,x,y), \min(14,5,2)) \)
  = \( \max(3, \min(2,x,y), 2) \)
  = \( \max(3, z, 2) \)   where  \(z = \min(2,x,y) \leq 2\)
  = \( 3 \)
  • I.e., we don’t need to know the values of \(x\) and \(y\)!

Minimax example, with \(\alpha{-}\beta\) pruning

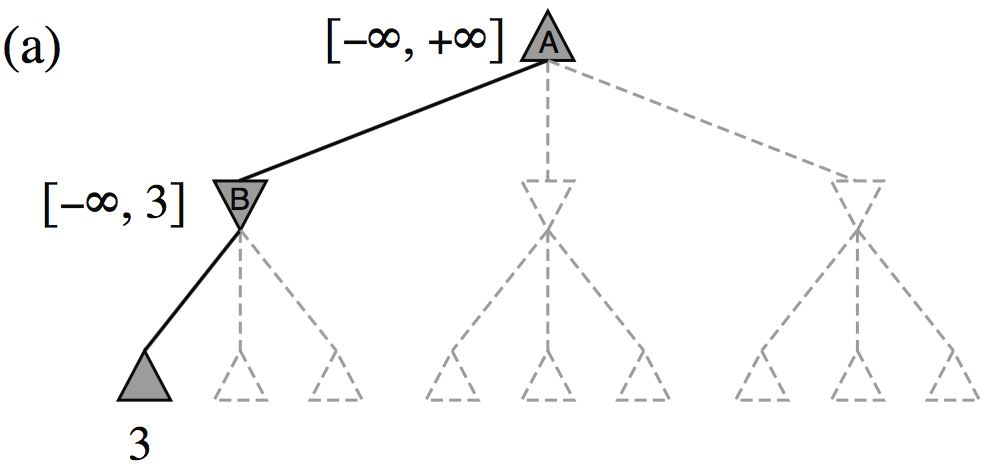
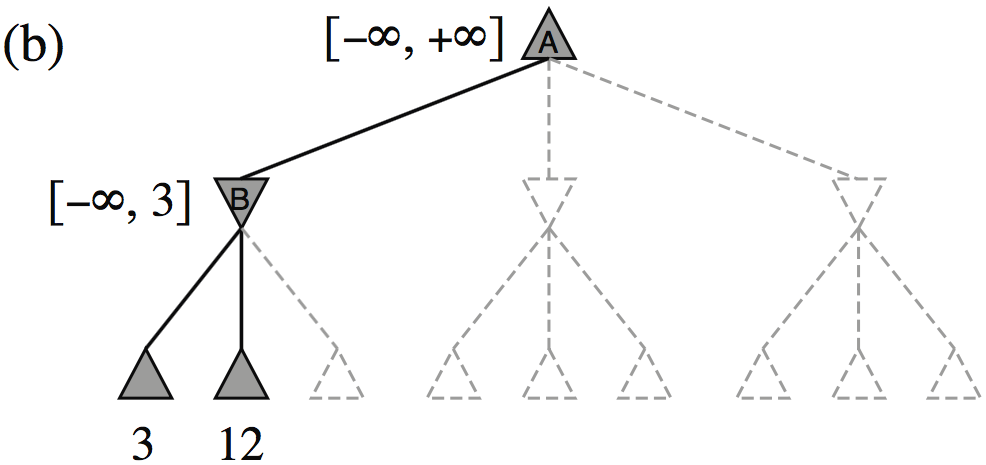
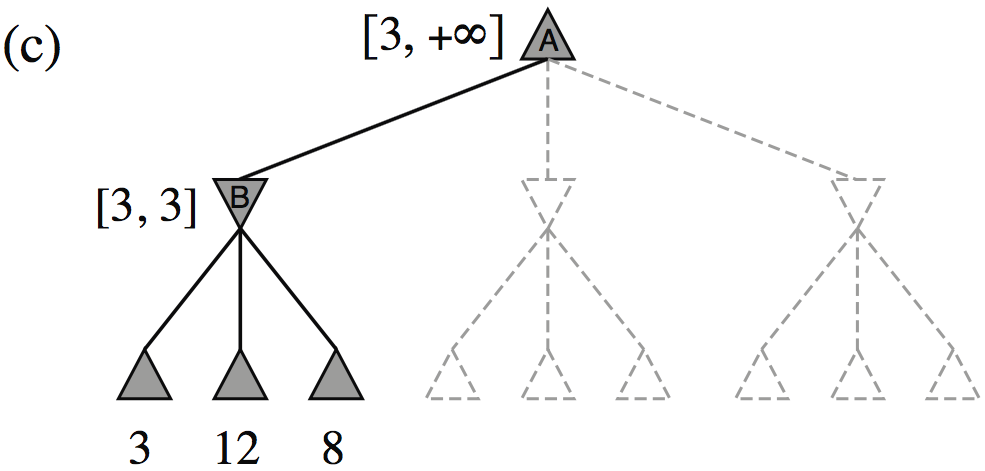
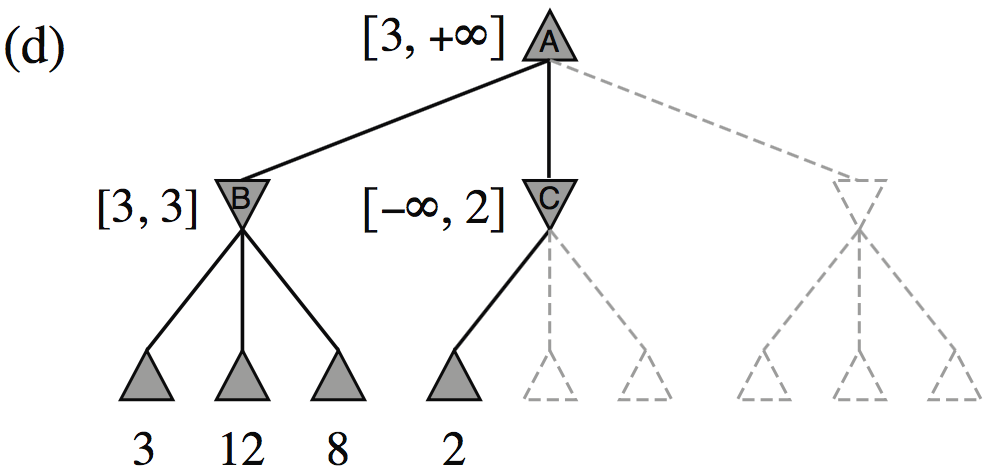
How efficient is \(\alpha{-}\beta\) pruning?

  • The amount of pruning provided by the α-β algorithm depends on the ordering of the children of each node.

    • It works best if a highest-valued child of a MAX node is selected first and
      if a lowest-valued child of a MIN node is returned first.

    • In real games, much of the effort is made to optimise the search order.

    • With a “perfect ordering”, the time complexity becomes \(O(b^{m/2})\)

      • this doubles the solvable search depth
      • however, \(35^{80/2}\) (for chess) or \(250^{160/2}\) (for go) is still quite large…

Minimax and real games

  • Most real games are too big to carry out minimax search, even with α-β pruning.

    • For these games, instead of stopping at leaf nodes,
      we have to use a cutoff test to decide when to stop.

    • The value returned at the node where the algorithm stops
      is an estimate of the value for this node.

    • The function used to estimate the value is an evaluation function.

    • Much work goes into finding good evaluation functions.

    • There is a trade-off between the amount of computation required
      to compute the evaluation function and the size of the search space
      that can be explored in any given time.

Imperfect decisions

Minimax vs H-minimax

  • function Minimax(state):
    • if TerminalTest(state) then return Utility(state)
    • A := Actions(state)
    • if state is a MAX node then return \(\max_{a\in A}\) Minimax(Result(state, a))
    • if state is a MIN node then return \(\min_{a\in A}\) Minimax(Result(state, a))
 
  • The Heuristic Minimax algorithm is similar to normal Minimax
    • it replaces TerminalTest and Utility with CutoffTest and Eval
 
  • function H-Minimax(state, depth):
    • if CutoffTest(state, depth) then return Eval(state)
    • A := Actions(state)
    • if state is a MAX node then return \(\max_{a\in A}\) H-Minimax(Result(state, a), depth+1)
    • if state is a MIN node then return \(\min_{a\in A}\) H-Minimax(Result(state, a), depth+1)

Evaluation functions

A naive evaluation function will not see the difference between these two states.

\[ Eval(s) = w_1 f_1(s) + w_2 f_2(s) + \cdots + w_n f_n(s) = \sum_{i=1}^{n} w_i f_i(s) \]

Problems with cutoff tests

  • Too simplistic cutoff tests and evaluation functions can be problematic:
    • e.g., if the cutoff is only based on the current depth
    • then it might cut off the search in unfortunate positions
      (such as (b) on the previous slide)
  •  
  • We want more sophisticated cutoff tests:
    • only cut off search in quiescent positions
    • i.e., in positions that are “stable”, unlikely to exhibit wild swings in value
    • non-quiescent positions should be expanded further

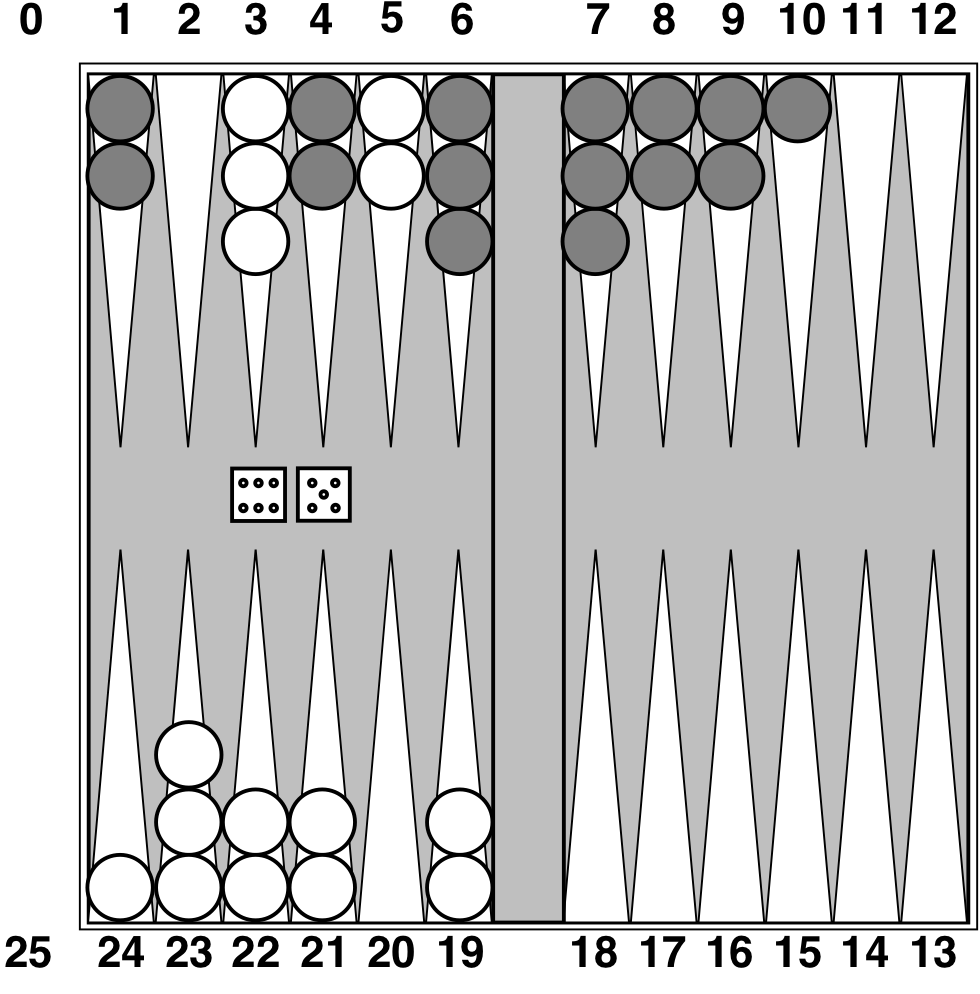
Stochastic games

Example: Backgammon

Stochastic games in general

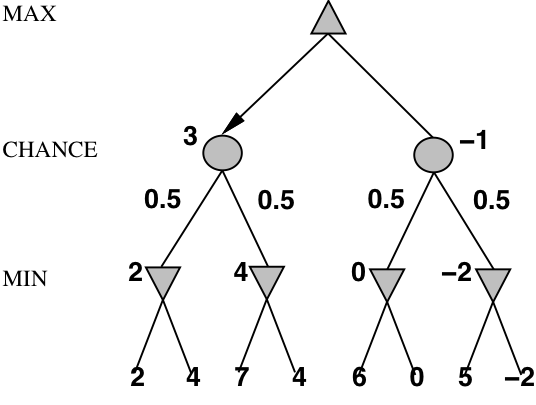
  • In stochastic games, chance is introduced by dice, card-shuffling, etc.
    • We introduce chance nodes to the game tree.
    • We can’t calculate a definite minimax value,
      instead we calculate the expected value of a position.
    • The expected value is the average of all possible outcomes.
  •  
  • A very simple example with coin-flipping and arbitrary values:

Algorithm for stochastic games

  • The ExpectiMinimax algorithm gives perfect play;
  • it’s just like Minimax, except we must also handle chance nodes:
 
  • function ExpectiMinimax(state):
    • if TerminalTest(state) then return Utility(state)
    • A := Actions(state)
    • if state is a MAX node then return \(\max_{a\in A}\) ExpectiMinimax(Result(state, a))
    • if state is a MAX node then return \(\min_{a\in A}\) ExpectiMinimax(Result(state, a))
    • if state is a chance node then return \(\sum_{a\in A}P(a)\)·ExpectiMinimax(Result(state, a))

where \(P(a)\) is the probability that action a occurs.

Constraint satisfaction problems (R&N 4.1, 7.1–7.5)

CSP as a search problem

Improving backtracking efficiency

Constraint propagation

Problem structure

Local search for CSP

CSP: Constraint satisfaction problems

  • CSP is a specific kind of search problem:
    • the state is defined by variables \(X_{i}\), each taking values from the domain \(D_{i}\)
    • the goal test is a set of constraints:
      • each constraint specifies allowed values for a subset of variables
      • all constraints must be satisfied
  •  
  • Differences to general search problems:
    • the path to a goal isn’t important, only the solution is.
    • there are no predefined starting state
    • often these problems are huge, with thousands of variables,
      so systematically searching the space is infeasible

Example: Map colouring (binary CSP)

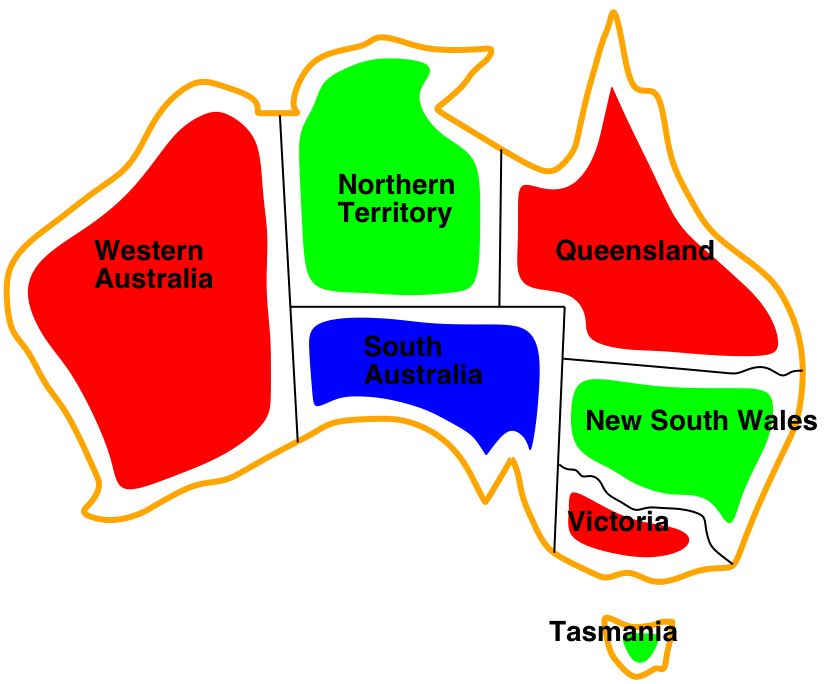
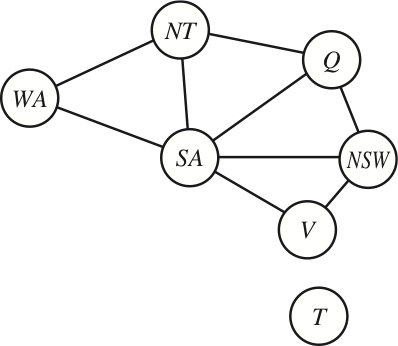
Variables: WA, NT, Q, NSW, V, SA, T
Domains: \(D_i\) = {red, green, blue}
Constraints: SA≠WA, SA≠NT, SA≠Q, SA≠NSW, SA≠V,
WA≠NT, NT≠Q, Q≠NSW, NSW≠V
Constraint graph: Every variable is a node, every binary constraint is an arc.

Example: Cryptarithmetic puzzle (higher-order CSP)

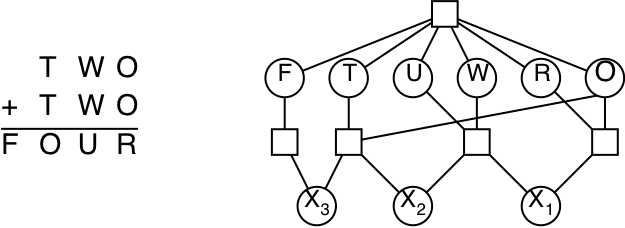
Variables: F, T, U, W, R, O, \(X_1, X_2, X_3\)
Domains: \(D_i\) = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
Constraints: Alldiff(F,T,U,W,R,O),  O+O=R+10·\(X_1\),   etc.
Constraint graph: This is not a binary CSP!
The graph is a constraint hypergraph.
  • At each depth level, decide on one single variable to assign:
    • this gives branching factor \(b=d\), so there are \(d^{n}\) leaves
  • Depth-first search with single-variable assignments is called backtracking search:
 
  • function BacktrackingSearch(csp):
    • return Backtrack(csp, { })
  •  
  • function Backtrack(csp, assignment):
    • if assignment is complete then return assignment
    • var := SelectUnassignedVariable(csp, assignment)
    • for each value in OrderDomainValues(csp, var, assignment):
      • if value is consistent with assignment:
        • inferences := Inference(csp, var, value)
        • if inferences ≠ failure:
          • result := Backtrack(csp, assignment \(\cup\) {var=value} \(\cup\) inferences)
          • if result ≠ failure then return result
    • return failure

Improving backtracking efficiency

  • The general-purpose algorithm gives rise to several questions:

    • Which variable should be assigned next?
      • SelectUnassignedVariable(csp, assignment)
    • In what order should its values be tried?
      • OrderDomainValues(csp, var, assignment)
    • What inferences should be performed at each step?
      • Inference(csp, var, value)

Selecting unassigned variables

  • Heuristics for selecting the next unassigned variable:

    • Minimum remaining values (MRV):
      \(\Longrightarrow\) choose the variable with the fewest legal values

    • Degree heuristic (if there are several MRV variables):
      \(\Longrightarrow\) choose the variable with most constraints on remaining variables

Ordering domain values

  • Heuristics for ordering the values of a selected variable:

    • Least constraining value:
      \(\Longrightarrow\) prefer the value that rules out the fewest choices
      for the neighboring variables in the constraint graph

Constraint propagation

Inference: Arc consistency, AC-3

  • Keep a set of arcs to be considered: pick one arc \((X,Y)\) at the time and make it consistent (i.e., make \(X\) arc consistent to \(Y\)).
    • Start with the set of all arcs \(\{(X,Y),(Y,X),(X,Z),(Z,X),\ldots\}\).
  •  
  • When an arc has been made arc consistent, does it ever need to be checked again?
    • An arc \((Z,X)\) needs to be revisited if the domain of \(X\) is revised.
 
  • function AC-3(inout csp):
    • initialise queue to all arcs in csp
    • while queue is not empty:
      • (X, Y) := RemoveOne(queue)
      • if Revise(csp, X, Y):
        • if   \(D_X=\emptyset\)   then return failure
        • for each Z in X.neighbors–{Y} do add (Z, X) to queue
  •  
  • function Revise(inout csp, X, Y):
    • delete every x from \(D_X\) such that there is no value y in \(D_Y\) satisfying the constraint \(C_{XY}\)
    • return true if \(D_X\) was revised

Combining backtracking with AC-3

  • What if some domains have more than one element after AC?

  • We can resort to backtracking search:

    • Select a variable and a value using some heuristics
      (e.g., minimum-remaining-values, degree-heuristic, least-constraining-value)
    • Make the graph arc-consistent again
    • Backtrack and try new values/variables, if AC fails
    • Select a new variable/value, perform arc-consistency, etc.

  • Do we need to restart AC from scratch?

    • no, only some arcs risk becoming inconsistent after a new assignment
    • restart AC with the queue \(\{(Y_i,X) | X\rightarrow Y_i\}\),
      i.e., only the arcs \((Y_i,X)\) where \(Y_i\) are the neighbors of \(X\)
    • this algorithm is called Maintaining Arc Consistency (MAC)

Consistency properties

  • There are several kinds of consistency properties and algorithms:

    • Node consistency: single variable, unary constraints (straightforward)

    • Arc consistency: pairs of variables, binary constraints (AC-3 algorithm)

    • Path consistency: triples of variables, binary constraints (PC-2 algorithm)

    • \(k\)-consistency: \(k\) variables, \(k\)-ary constraints (algorithms exponential in \(k\))

    • Consistency for global constraints:
      Special-purpose algorithms for different constraints, e.g.:

      • Alldiff(\(X_1,\ldots,X_m\)) is inconsistent if \(m > |D_1\cup\cdots\cup D_m|\)
      • Atmost(\(n,X_1,\ldots,X_m\)) is inconsistent if \(n < \sum_i \min(D_i)\)

Problem structure

Tree-structured CSP

(will not be in the written examination)

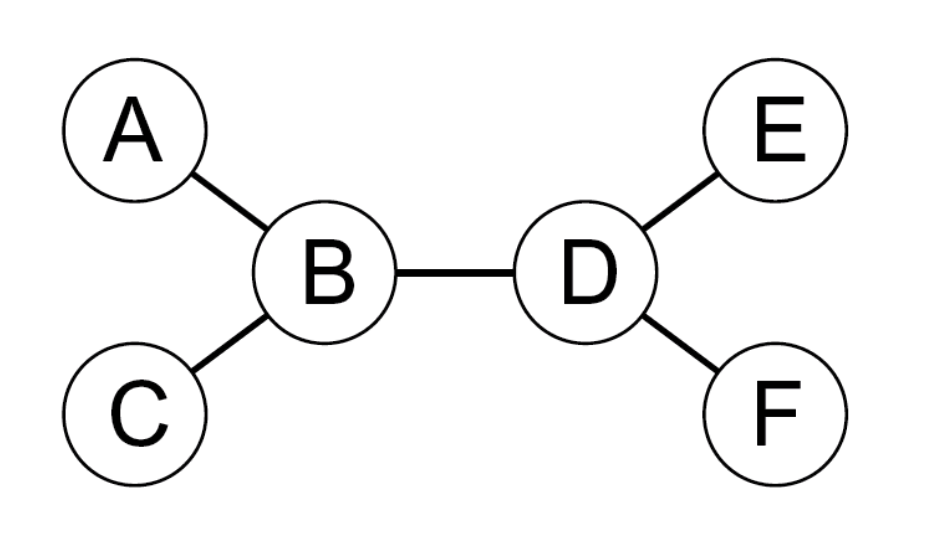
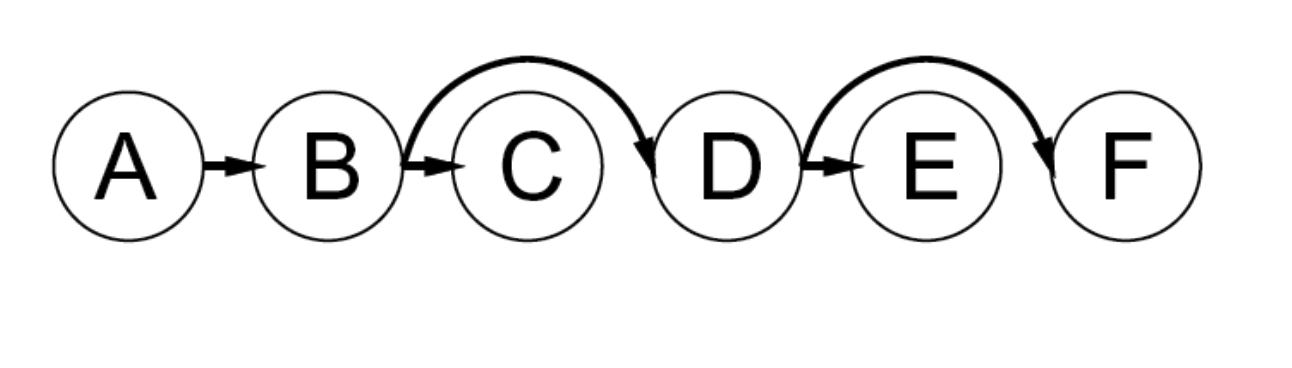
  • A constraint graph is a tree when any two variables are connected by only one path.
    • then any variable can act as root in the tree
    • tree-structured CSP can be solved in linear time, in the number of variables!
  •  
  • To solve a tree-structured CSP:
    • first pick a variable to be the root of the tree
    • then find a topological sort of the variables (with the root first)
    • finally, make each arc consistent, in reverse topological order

Converting to tree-structured CSP

(will not be in the written examination)

  • Most CSPs are not tree-structured, but sometimes we can reduce them to a tree
    • one approach is to assign values to some variables,
      so that the remaining variables form a tree

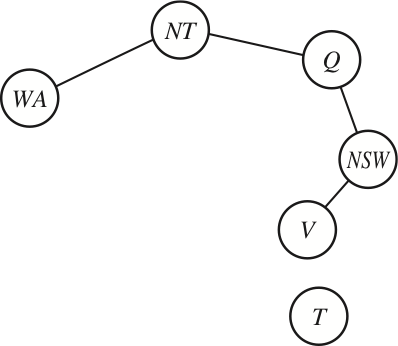
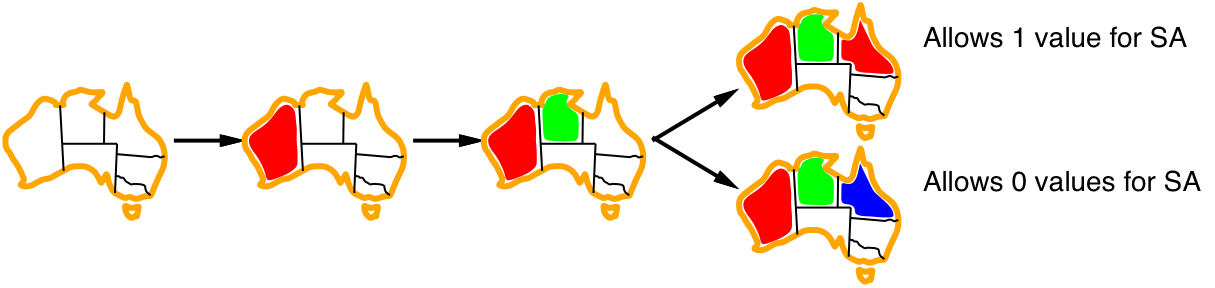
  • If we assign a colour to South Australia, then the remaining variables form a tree

    • An alternative is to assign values to {NT,Q,V}: But this is worse than assigning South Australia, because then we have to try 3×3×3 different assignments, and for each of them solve the remaining tree-CSP

Local search for CSP

  • Given an assignment of a value to each variable:
    • A conflict is an unsatisfied constraint.
    • The goal is an assignment with zero conflicts.
    • Heuristic function to be minimized: the number of conflicts.
      • this is the min-conflicts heuristics
 
  • function MinConflicts(csp, max_steps)
    • current := an initial complete assignment for csp
    • repeat max_steps times:
      • if current is a solution for csp then return current
      • var := a randomly chosen conflicted variable from csp
      • value := the value v for var that minimises Conflicts(var, v, current, csp)
      • current[var] = value
    • return failure

Example: \(n\)-queens (revisited)

  • Put \(n\) queens on an \(n\times n\) board, in separate columns
  • Conflicts = unsatisfied constraints = n:o of threatened queens
  • Move a queen to reduce the number of conflicts
    • repeat until we cannot move any queen anymore
    • then we are at a local maximum — hopefully it is global too

Example: Travelling salesperson

  • Start with any complete tour, and perform pairwise exchanges

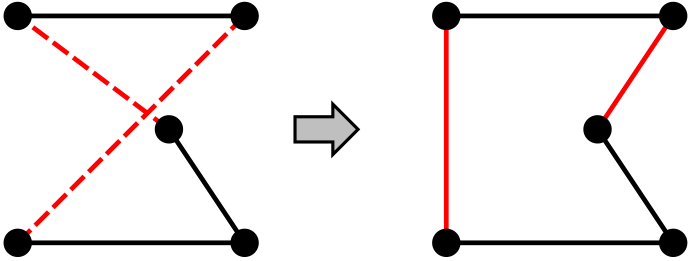
  • Variants of this approach get within 1% of optimal
    very quickly with thousands of cities

Hill climbing search is also called gradient/steepest ascent/descent,
or greedy local search.

  • function HillClimbing(graph, initialState):
    • current := initialState
    • loop:
      • neighbor := a highest-valued successor of current
      • if neighbor.value ≤ current.value then return current
      • current := neighbor

Problems with hill climbing

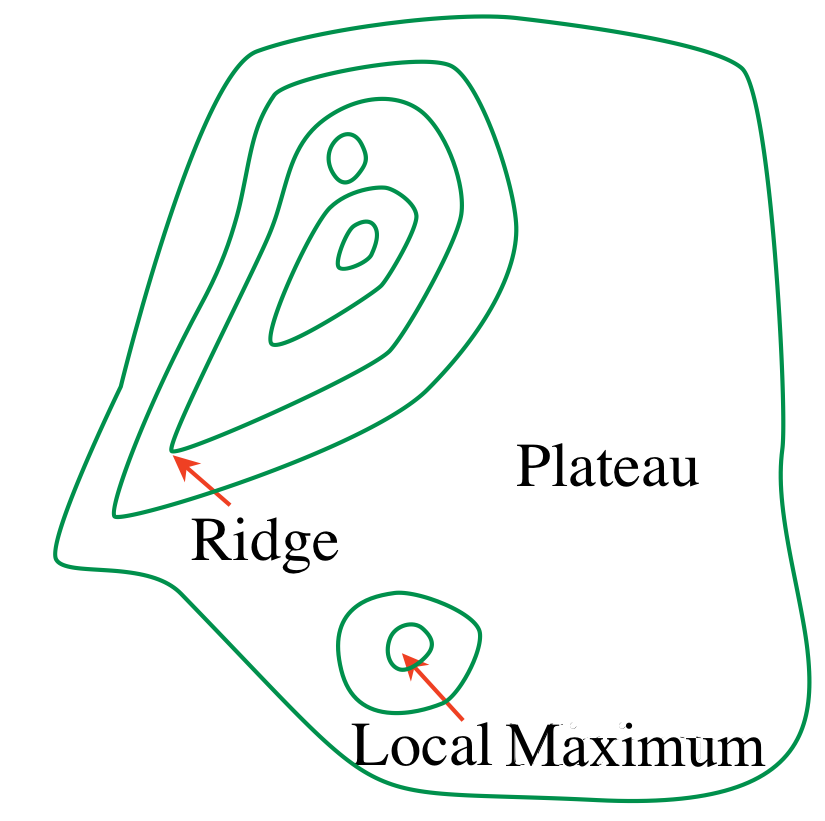
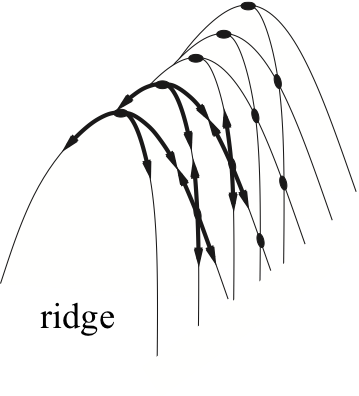
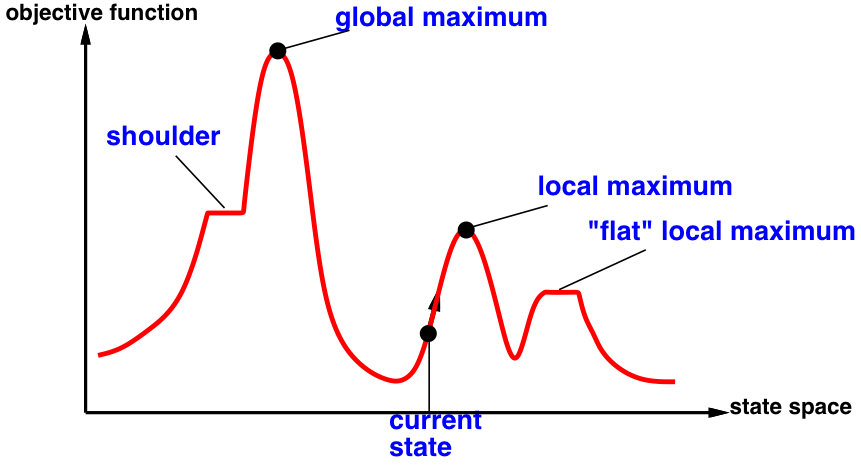
Local maxima   —   Ridges   —   Plateaux

    

Randomized hill climbing

  • As well as upward steps we can allow for:

    • Random steps: (sometimes) move to a random neighbor.

    • Random restart: (sometimes) reassign random values to all variables.

  • Both variants can be combined!

1-dimensional illustrative example

  • Two 1-dimensional search spaces; you can step right or left:

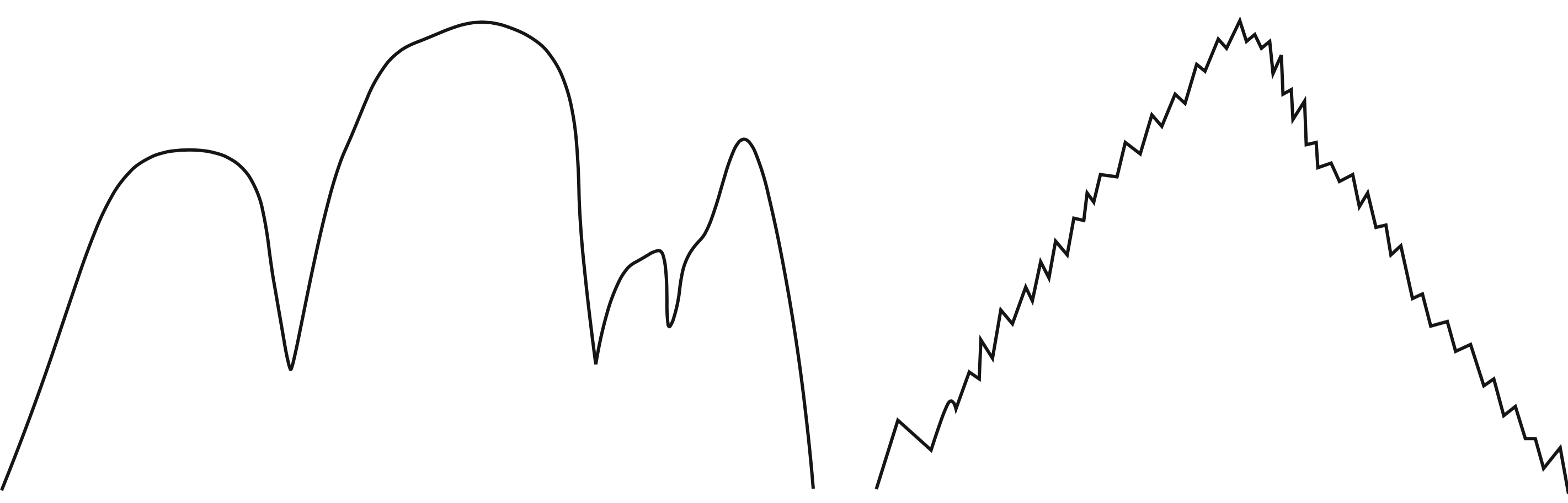
  • Which method would most easily find the global maximum?
    • random steps or random restarts?
  • What if we have hundreds or thousands of dimensions?
    • …where different dimensions have different structure?